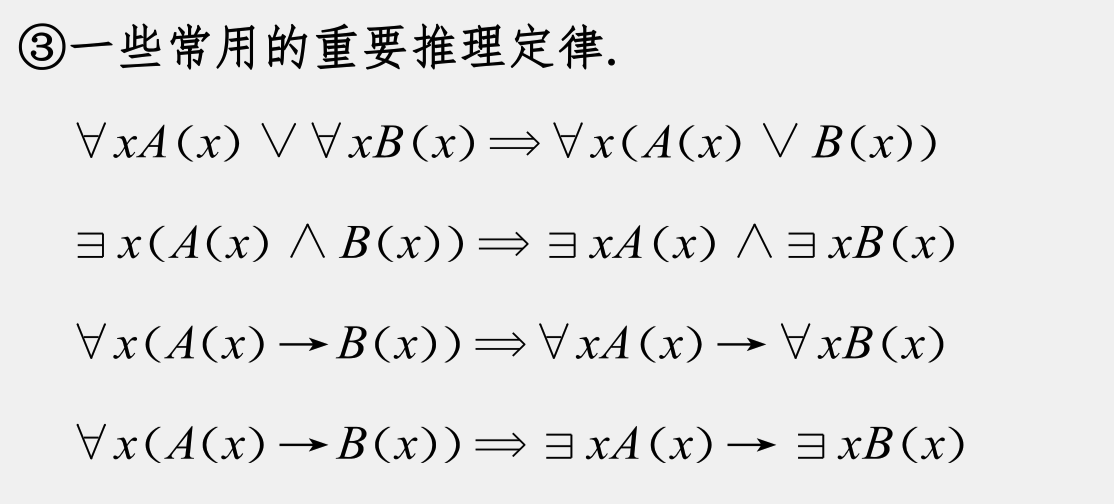[TOC]

命题逻辑
命题联结词
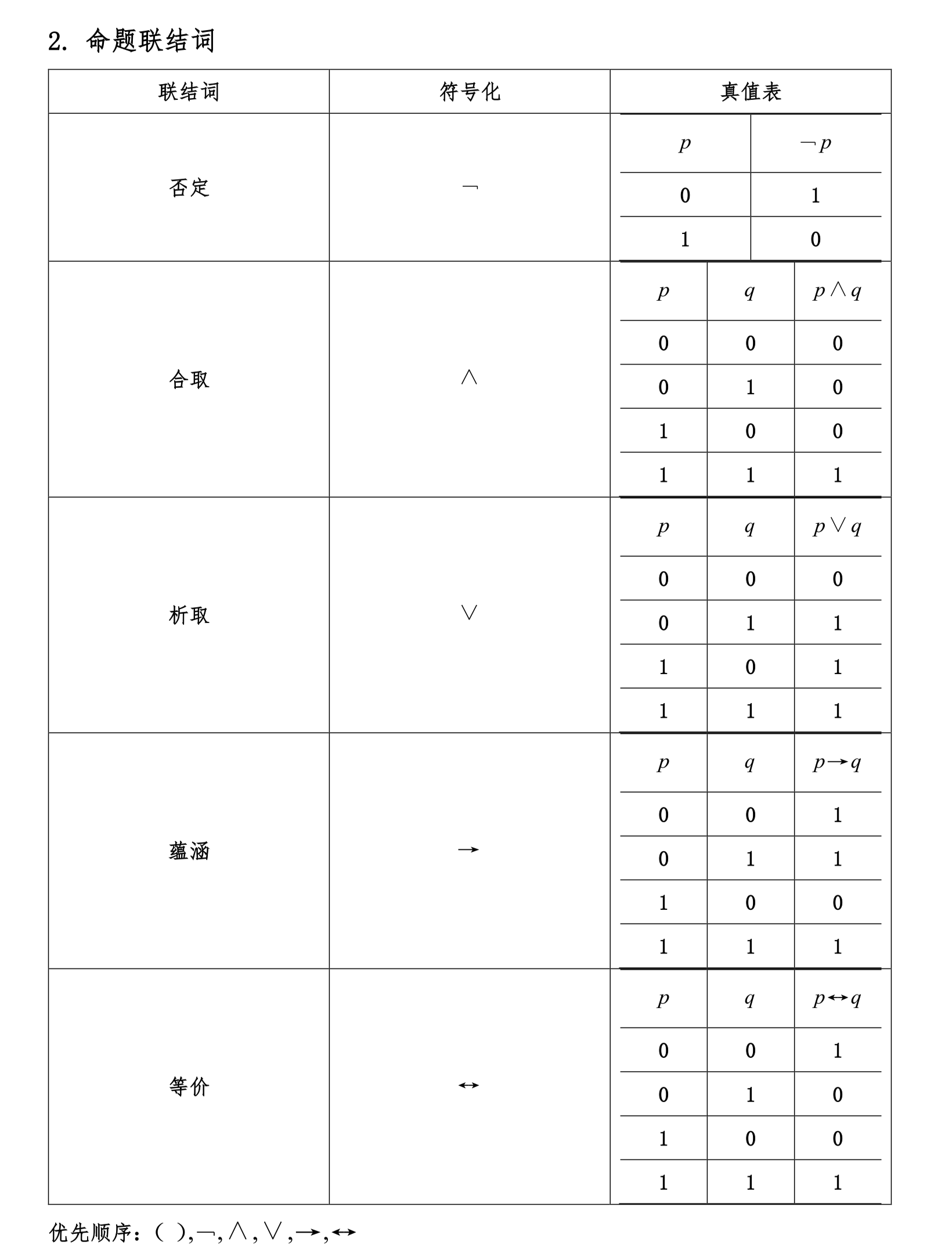

等值式


命题逻辑的推理

谓词逻辑等值式


注意 :
使用论域消去量词

消去的时候先消去离谓词近的那一个量词
常用推理定律
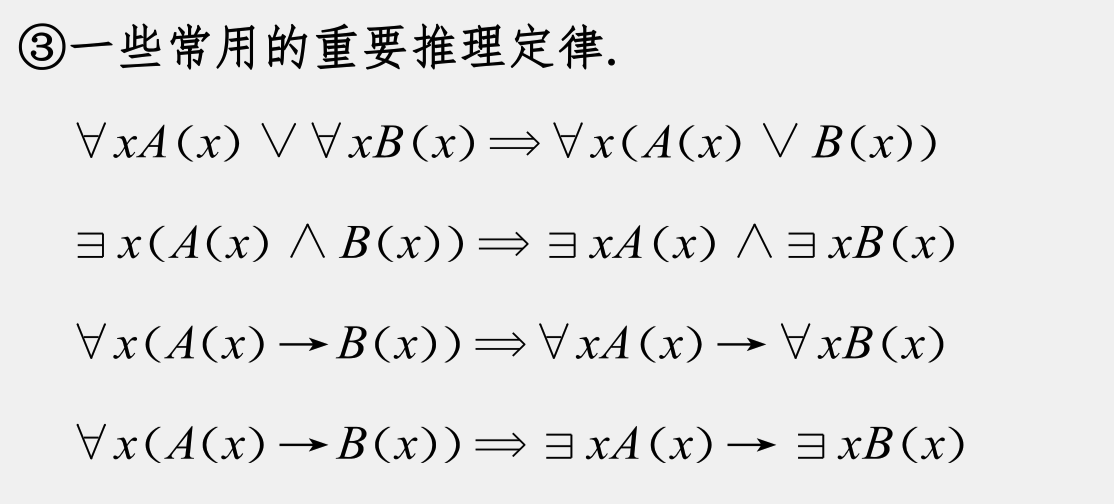
后两个表达式展示了在逻辑推理中,不同量词(全称量词 ∀ 和存在量词 ∃ )的使用对逻辑命题的影响。
- 第一个表达式:
∀x(A(x)→B(x))⟹∀xA(x)→∀xB(x)
这个表达式表示:如果对于所有的 x,命题 A(x) 蕴含命题 B(x),那么如果所有的 x 都满足 A(x),则所有的 x 都满足 B(x)。换句话说,如果 A(x) 对 x 的每个实例都蕴含 B(x),那么 A(x) 对所有 x 成立时 B(x) 也对所有 x 成立。
2. 第二个表达式:
∀x(A(x)→B(x))⟹∃xA(x)→∃xB(x)
这个表达式表示:如果对于所有的 x,命题 A(x) 蕴含命题 B(x),那么如果存在某个 x 满足 A(x),则存在某个 x 满足 B(x)。换句话说,如果 A(x) 对 x 的每个实例都蕴含 B(x),那么如果有至少一个 x 使得 A(x) 成立,则有至少一个 x 使得 B(x) 成立。
这两个表达式的区别在于结论中的量词:
- 第一个表达式的结论涉及全称量词 ∀,表示所有的 x 都必须满足某个条件。
- 第二个表达式的结论涉及存在量词∃,表示至少有一个 x 满足某个条件。
这两个表达式虽然前提相同,但由于结论中的量词不同,表达的含义也不同。在逻辑推理中,量词的变化会显著影响命题的含义和推理过程。
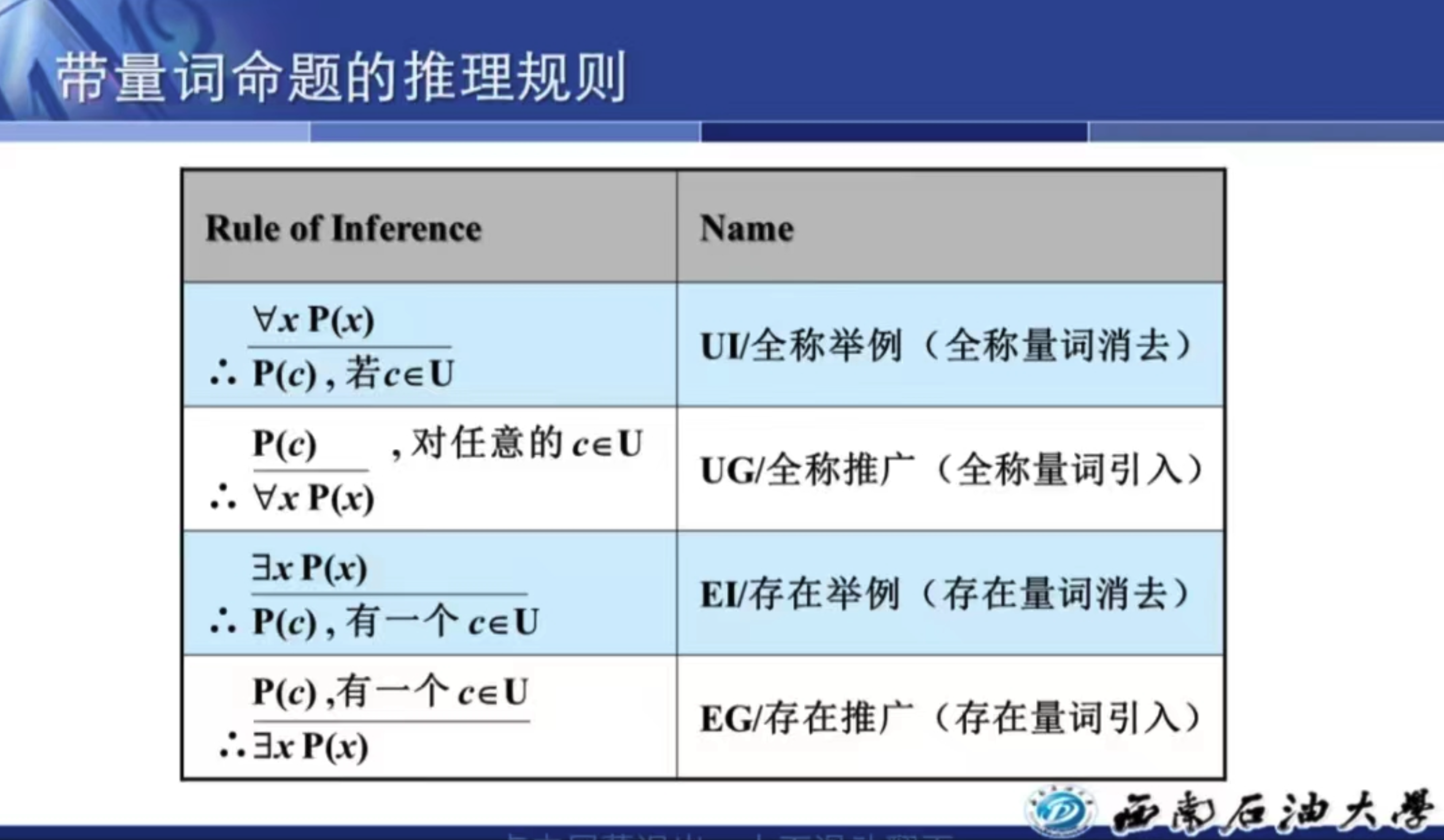
量词消去与引入

存在量词消去(Existential Elimination)
存在量词消去规则允许我们从一个存在量词的命题中推导出一个不含量词的命题。形式化地,如果我们知道 ∃xP(x) 为真,那么我们可以引入一个新的常量 c,使�得 P(c) 为真。
规则形式:
P(c)∃xP(x)
注意事项:
- 常量 c 必须是一个新的符号,即它在当前推理过程中之前没有出现过。
例子:
假设我们知道 ∃x(x>0),那么我们可以引入一个新的常量 c,使得 c>0。
存在量词引入(Existential Introduction)
存在量词引入规则允许我们从一个具体的命题推导出一个存在量词的命题。形式化地,如果我们知道 P(c) 为真,那么我们可以推导出 ∃xP(x)。
规则形式:
∃xP(x)P(c)
注意事项:
例子:
假设我们知道 c>0,那么我们可以推导出 ∃x(x>0)。
全称量词消去(Universal Elimination)
全称量词消去规则允许我们从一个全称量词的命题中推导出一个具体的命题。形式化地,如果我们知道 ∀xP(x) 为真,那么对于任意对象 a,P(a) 也为真。
规则形式:
P(a)∀xP(x)
注意事项:
- 对象 a 可以是任何对象,包括变量、常量或函数项。
例子:
假设我们知道 ∀x(x≥0),那么对于任意 a,我们可以推导出 a≥0。
全称量词引入(Universal Introduction)
全称量词引入规则允许我们从一个具体的命题推导出一个全称量词的命题。形式化地,如果对于任意对象 a,P(a) 为真,那么我们可以推导出 ∀xP(x)。
规则形式:
∀xP(x)P(a) for arbitrary a
注意事项:
- 对象 a 必须是任意的,即在推理过程中它不能有任何特定的属性或限制。
例子:
假设我们能够证明对于任意 a,a2≥0,那么我们可以推导出 ∀x(x2≥0)。


附加前提引入




集合中的明确写出来的空集看作是一个符号就行
集合的运算

包含排斥原理(容斥原理)
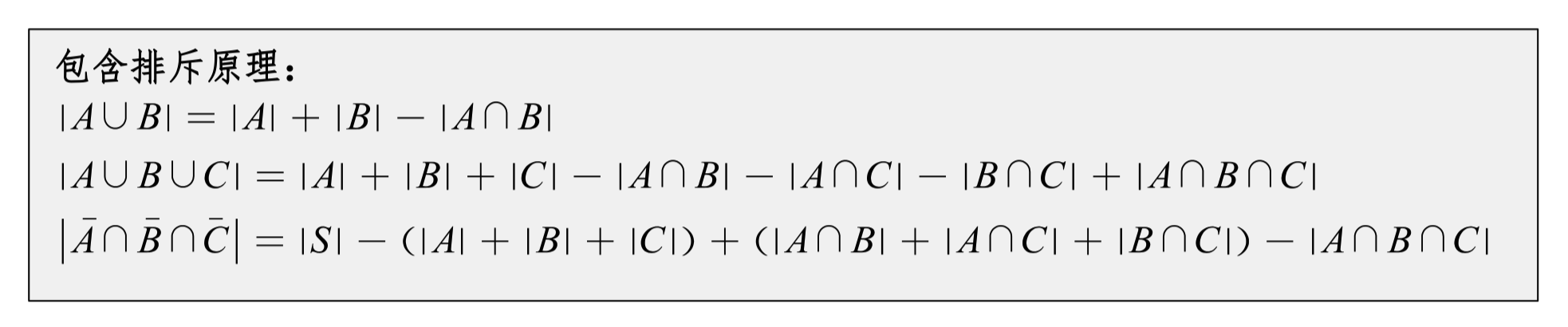
集合恒等式



二元关系

笛卡尔积不满足交换率


二元关系


关系的运算


关系的性质
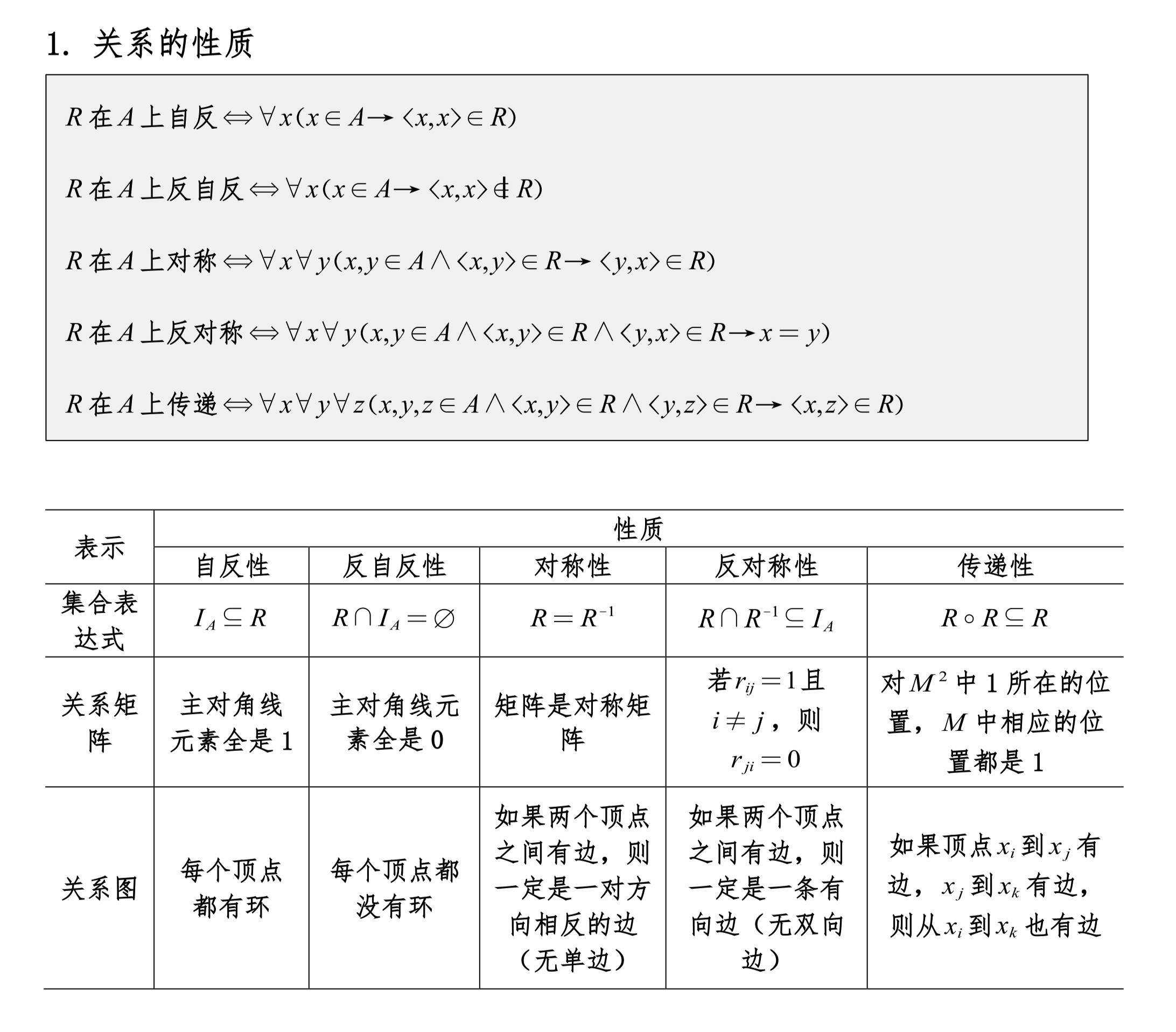
{(a,b),(b,c)}的传递闭包是什么
给定关系R={(a,b),(b,c)},我们需要找到它的传递闭包。传递闭包是指在原关系的基础上,加入所有能够通过传递性得到的关系对,使其成为传递的。
传递闭包R+的定义是:如果(x,y)∈R+且(y,z)∈R+,则(x,z)∈R+。
首先,原关系R中的元素有:
R={(a,b),(b,c)}
接下来,检查通过传递性能够得到的关系对:
- (a,b)∈R且(b,c)∈R,则根据传递性(a,c)也必须在传递闭包中。
因此,传递闭包R+是:
R+={(a,b),(b,c),(a,c)}
所以,关系R={(a,b),(b,c)}的传递闭包是:
R+={(a,b),(b,c),(a,c)}
设集合 A 有 3 个元素,则 A 上可定义的等价关系的个数为( )。
等价关系是将集合划分为若干个不相交的子集。等价关系的个数等于集合 A 的所有可能划分的个数,即所谓的 Bell 数。
对集合 A={a,b,c},计算其 Bell 数。
我们依次考察集合 {1,2,3} 的所有可能划分。设有:
- 一个子集:{{a,b,c}}
- 两个子集:{{a},{b,c}},{{b},{a,c}},{{c},{a,b}}
- 三个子集:{{a},{b},{c}}
具体计算方法如下:
- B1=1 (1 个元素的集合只有一种划分)
- B2=2 (2 个元素的集合有两种划分:全体一个集合或分成两个单元素集合)
- B3 是需要计算的。
使用 Bell 数递归公式:
Bn+1=∑k=0n(kn)Bk
具体计算 B3:
B3=∑k=02(k2)Bk
计算过程:
B3=(02)B0+(12)B1+(22)B2
B3=1⋅1+2⋅1+1⋅2
B3=1+2+2
B3=5
因此,集合 A 上可定义的等价关系的个数为 5。
答案是:5
在数学中,上取整和下取整分别使用不同的符号来表示。
-
上取整(Ceiling function):
- 符号:⌈x⌉
- 含义:将数值 x 向上取整到最接近的整数。如果 x 本身是整数,则结果是 x 自身。例如:⌈3.2⌉=4,⌈−2.7⌉=−2。
-
下取整(Floor function):
- 符号:⌊x⌋
- 含义:将数值 x 向下取整到最接近的整数。如果 x 本身是整数,则结果是 x 自身。例如:⌊3.8⌋=3,⌊−2.3⌋=−3。
这两个符号用于表示对数值进行向上或向下取整的操作,在数学和计算机科学中广泛应用。



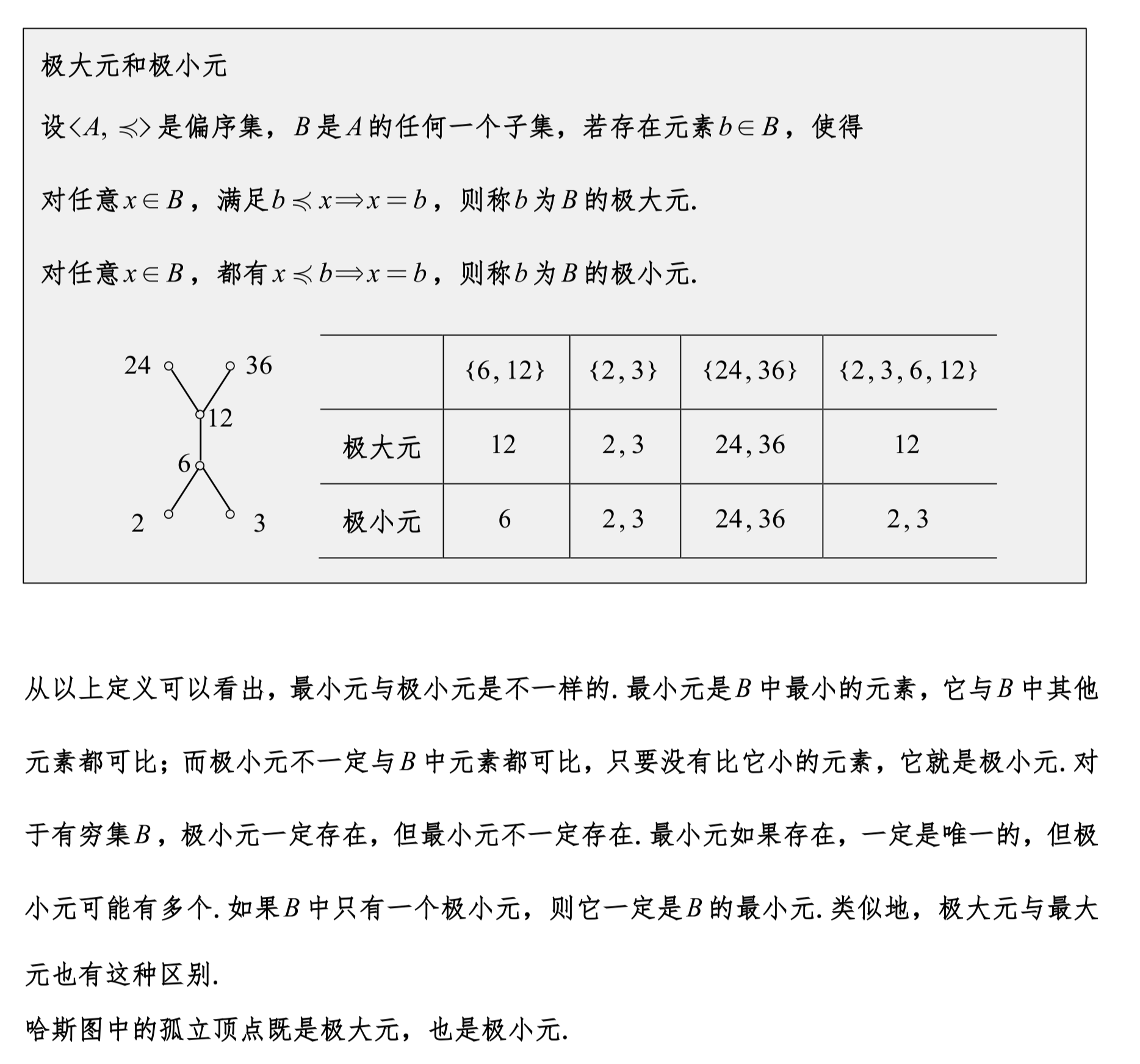
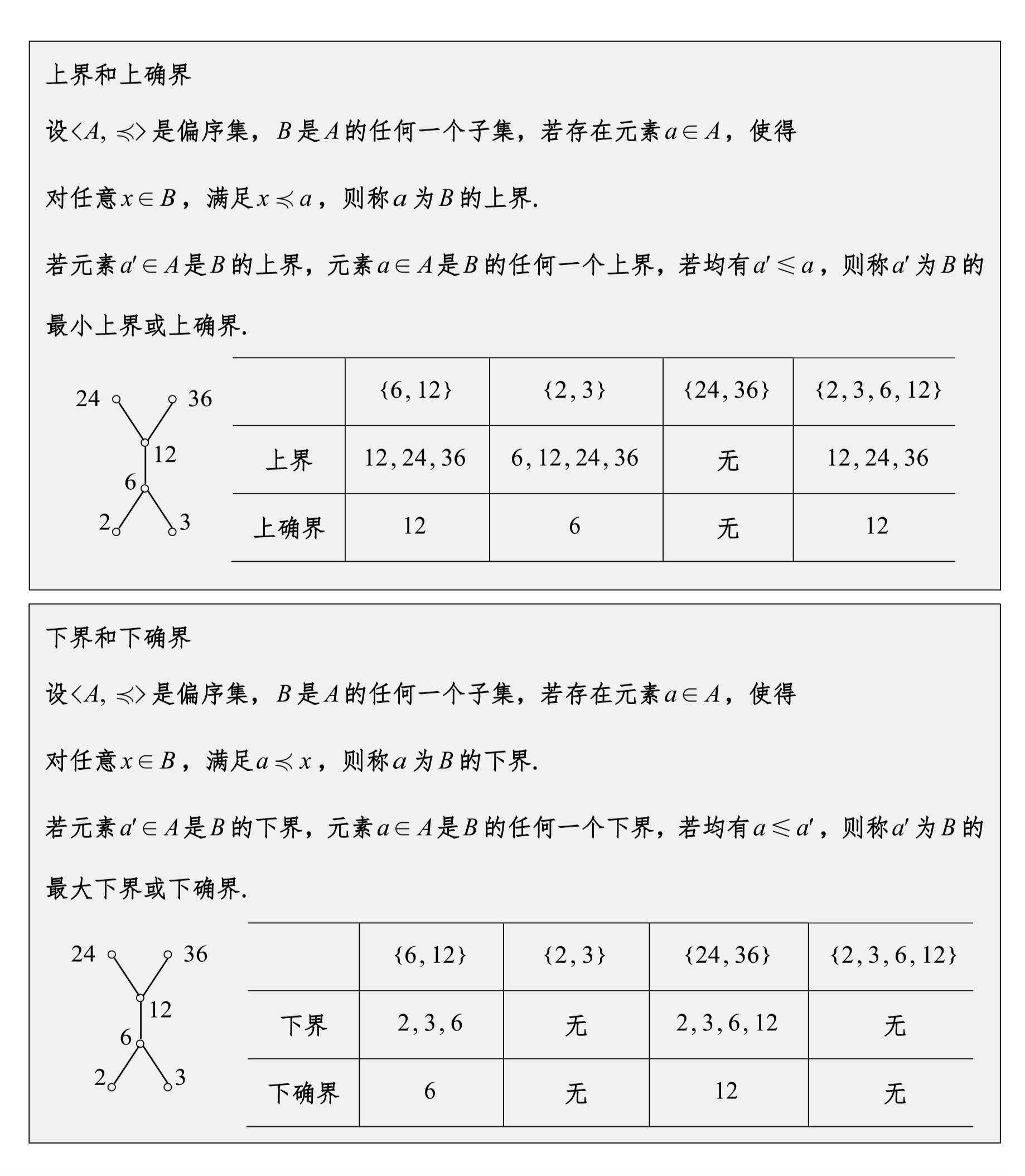
注意⚠️
极、最都是在给定的集合内进行寻找
而确界是在整个哈斯图中寻找
不可比就没有最,但是可能有极
这两种概念��中都有’大于等于‘、’小于等于‘的概念,千万不要忘记等于

握手定理

图的度数和定理
首先,我们需要理解一些基本概念:
- 顶点的度数:一个顶点的度数是与该顶点相连的边的数目。
- 图的度数和:图中所有顶点的度数之和等于图中所有边数的两倍。
图的度数和定理可以表述为:
∑v∈Vdeg(v)=2∣E∣
其中,deg(v) 表示顶点 v 的度数,V 是图的顶点集,E 是图的边集。
奇数和偶数的性质
- 奇数加奇数等于偶数。
- 奇数加偶数等于奇数。
- 偶数加偶��数等于偶数。
证明奇度顶点的个数是偶数
根据度数和定理,图中所有顶点的度数之和是一个偶数 2∣E∣。
现在,考虑将所有顶点的度数分为两类:奇数度顶点和偶数度顶点。
设图中有 k 个奇度顶点。由于偶数度顶点的度数之和显然是偶数,我们可以用 S奇 和 S偶 分别表示奇数度顶点和偶数度顶点的度数之和,那么:
S奇+S偶=2∣E∣
其中 S偶 是偶数(因为偶数个偶数的和是偶数),而 2∣E∣ 也是偶数。
因此,S奇 必须也是偶数,因为偶数减偶数还是偶数。
考虑到奇数的和只有在奇数个奇数相加时才是奇数,在偶数个奇数相加时是偶数,因此,S奇 是偶数意味着奇度顶点的个数 k 必须是偶数。
任何图中的奇度顶点的个数总是偶数。这是因为图中所有顶点的度数之和是偶数,并且只有偶数个奇数相加的结果才是偶数,从而奇数个奇数相加不可能是偶数。
度序列

判断能作为图的度序列的方法
总度数一定为偶数
奇度顶点个数为偶数个
最大度数小于n-1,无向简单图中跟一个顶点相连的顶点最多就是n-1个
完全无向图

u到v存在通路称作u到可达,, 注意是存在通路就行

无向图的矩阵表示
行数是顶点的个数,列数是边的个数

有向图的矩阵表示

邻接矩阵
数学归纳法
数学归纳法的步骤
-
基础步骤(Base Step):
- 证明命题在第一个值(通常是n=1)成立。
-
归纳步骤(Inductive Step):
- 假设命题在某个值k成立,即假设命题对n=k成立。
- 在此假设下,证明命题对n=k+1也成立。
如果这两个步骤都完成了,那么根据数学归纳法,命题在所有正整数n上都成立。
做题步骤总��结
- 基础步骤:验证命题在n=1时是否成立。
- 归纳假设:假设命题在n=k时成立。
- 归纳步骤:在归纳假设下,证明命题在n=k+1时也成立。
例子:证明1+2+3+⋯+n=2n(n+1)
基础步骤
我们首先证明当n=1时命题成立。
左边:1
右边:21(1+1)=22=1
左边等于右边,所以命题在n=1时成立。
归纳步骤
假设命题在n=k时成立,即假设:
1+2+3+⋯+k=2k(k+1)
在此假设下,我们需要证明命题在n=k+1时也成立。即我们需要证明:
1+2+3+⋯+k+(k+1)=2(k+1)((k+1)+1)
根据归纳假设,左边可以写成:
(1+2+3+⋯+k)+(k+1)=2k(k+1)+(k+1)
我们来简化右边:
2k(k+1)+(k+1)=2k(k+1)+2(k+1)=2(k+1)(k+2)
这正是我们需要证明的右边形式:
2(k+1)((k+1)+1)
因此,归纳步骤也完成了。
容斥原理






我们的问题是求解方程 x1+x2+x3=11 的非负整数解。这里不考虑任何约束条件。这个问题可以转化为组合数学中的“隔板法”。
隔板法解释
要将 11 个单位分成 3 组,我们可以使用 2 个隔板,将 11 个单位分成 3 份。因此,问题转化为在 11 个单位中插入 2 个隔板的问题。
例如,11 个单位可以表示为:
∙∙∙∙∙∙∙∙∙∙∙
我们需要在这些单位中插入 2 个隔板,比如插入在第 4 和第 8 个单位之后,就可以得到:
∙∙∙∙∣∙∙∙∙∣∙∙∙
这样,我们就将 11 个单位分成了三部分,每部分代表 x1、x2 和 x3 的值。
数学公式推导
上述问题相当于在 11 个单位中选择 2 个位置放置隔板的问题。这是一个组合问题,其公式为:
N=(r−1n+r−1)
其中,n 是单位的数量,r 是变量的数量。对于我们的例子:
- n=11(总单位数)
- r=3(变量数)
所以,我们需要计算:
N=(3−111+3−1)=(213)
计算组合数
计算组合数 (213) 的公式是:
(213)=2!(13−2)!13!=2×113×12=78
因此,总的非负整数解的数量 N 是 78。
首先,题目要求的是 x1+x2+x3=11 有多少个非负整数解,其中 x1≤3、x2≤4、x3≤6。
使用容斥原理,设:
- 性质 P1 为 x1>3
- 性质 P2 为 x2>4
- 性质 P3 为 x3>6
要计算满足这些不等式约束的解的数量,使用容斥原理公式:
N(P1′P2′P3′)=N−N(P1)−N(P2)−N(P3)+N(P1P2)+N(P1P3)+N(P2P3)−N(P1P2P3)
其中,N 是总的非负整数解的数量,不考虑约束条件:
N=(113+11−1)=(1113)=78
接下来我们重点解释 N(P1) 的求法,即 x1>3 的解的数量:
求 N(P1)
条件 x1>3 意味着 x1 至少为 4。因此我们可以设 x1′=x1−4,于是 x1′≥0。
将 x1 替换为 x1′ 后,原方程变为:
x1′+4+x2+x3=11⟹x1′+x2+x3=7
现在问题变成了求 x1′+x2+x3=7 的非负整数解的数量。
这个问题的解的数量是:
N(P1)=(73+7−1)=(79)=36
类似地,求 N(P2) 和 N(P3)
-
N(P2) 对应的是 x2>4,设 x2′=x2−5,则变为求 x1+x2′+x3=6 的解:
N(P2)=(63+6−1)=(68)=28
-
N(P3) 对应的是 x3>6,设 x3′=x3−7,则变为求 x1+x2+x3′=4 的解:
N(P3)=(43+4−1)=(46)=15
使用容斥原理求解最终结果
将所有的 N(P1), N(P2), N(P3), 以及各个组合代入容斥原理公式,计算最终结果:
N(P1′P2′P3′)=78−36−28−15+N(P1P2)+N(P1P3)+N(P2P3)−N(P1P2P3)
其中 N(P1P2),N(P1P3),N(P2P3),和 N(P1P2P3) 的求法与上述类似,只是方程右侧的值会进一步减小。
递推关系

当然可以,下面我将详细讲解递推关系的求解步骤,并使用 LaTeX 格式化公式。
1. 写出递推关系式
题目给出的递推关系是:
an=−5an−1−6an−2+42⋅4n
2. 确定特征方程
为了求解齐次部分,我们先忽略非齐次项,得到对应的齐次递推关系:
an(h)=−5an−1−6an−2
写出特征方程,假设 an(h)=rn,代入齐次递推关系式:
rn=−5rn−1−6rn−2
将方程两边同除以 rn−2:
r2=−5r−6
得到特征方程:
r2+5r+6=0
3. 解特征方程
解特征方程:
r2+5r+6=0
使用二次方程求根公式 r=2a−b±b2−4ac,其中 a=1,b=5,c=6:
r=2−5±25−24
r=2−5±1
得到两个根:
r1=−2,r2=−3
4. 齐次解的通解
由于特征方程有两个不同的实根 −2 和 −3,齐次解的通解为:
an(h)=α(−2)n+β(−3)n
其中,α 和 β 是待定常数。
5. 求特解
现在求非齐次部分的特解。非齐次项是 42⋅4n。我们假设特解的形式为:
an(p)=c⋅4n
6. 代入原递推关系求解特解
将假设的特解代入原递推关系式:
c⋅4n=−5c⋅4n−1−6c⋅4n−2+42⋅4n
将方程两边同除以 4n−2:
16c=−20c−6c+672
解此方程:
16c=−26c+672
42c=672
c=16
因此,特解为:
an(p)=16⋅4n
7. 原递推关系的通解
总解由齐次解和特解之和组成:
an=an(h)+an(p)
an=α(−2)n+β(−3)n+16⋅4n
8. 利用初始条件求解常数
用初始条件 a1=56 和 a2=278 来求解 α 和 β。
对于 n=1:
56=α(−2)+β(−3)+16⋅4
56=−2α−3β+64
−2α−3β=−8(1)
对于 n=2:
278=α(−2)2+β(−3)2+16⋅42
278=4α+9β+256
4α+9β=22(2)
解方程组 (1) 和 (2):
−2α−3β=−8
4α+9β=22
先解第一个方程:
−6α−9β=−24(3)
然后将 (3) 和 (2) 相加:
4α+9β+(−6α−9β)=22−24
−2α=−2
α=1
代入方程 (1) 求 β:
−2(1)−3β=−8
−2−3β=−8
3β=6
β=2
9. 最终解
代入 α 和 β 的值:
an=(−2)n+2(−3)n+16⋅4n
通过以上详细步骤,我们成功求解了递推关系。总结起来
基于幂次的传递闭包算法

基于0-1矩阵幂次的传递闭包算法是一种用于计算关系传递闭包的方法。传递闭包是指在一个关系中,如果存在从元素a到元素b的路径,那么传递闭包关系中也包含a到b的直接关系。基于0-1矩阵幂次的方法是通过矩阵乘法来计算传递闭包的。
具体算法步骤如下:
-
初始化矩阵:
- 首先将关系R表示成一个0-1矩阵A。对于集合{a,b,c,d,e},矩阵A的大小为5×5。
- 如果(a,b)∈R,则A中对应位置的元素为1,否则为0。
-
计算矩阵幂次:
- 计算A的幂次矩阵 A2,A3,…,An,直到矩阵不再变化。矩阵的幂次计算采用布尔乘法,即在乘法过程中,1和1相乘结果仍为1,0和任何数相乘结果为0。
-
计算��传递闭包:
- 传递闭包矩阵B可以通过将所有幂次矩阵进行或运算(逻辑或)得到,即 B=A∨A2∨A3∨…∨An。
示例计算:
给定集合{a,b,c,d,e}和关系 R={(a,c),(b,d),(c,a),(d,b),(e,d)},首先将其转换成0-1矩阵A:
A=0010000010100000100100000
接下来计算A的幂次矩阵:
A2=A×A=1000001001001000001000000
A3=A×A2=A=0010000010100000100100000
由于 A4=A2 和 A5=A3,可以停止计算。
最后计算传递闭包矩阵B:
B=A∨A2=1010001011101000101100000
因此,关系R的传递闭包的0-1矩阵B为:
B=1010001011101000101100000
通过上述步骤,我们可以得到关系R的传递闭包的0-1矩阵。
传递闭包错题
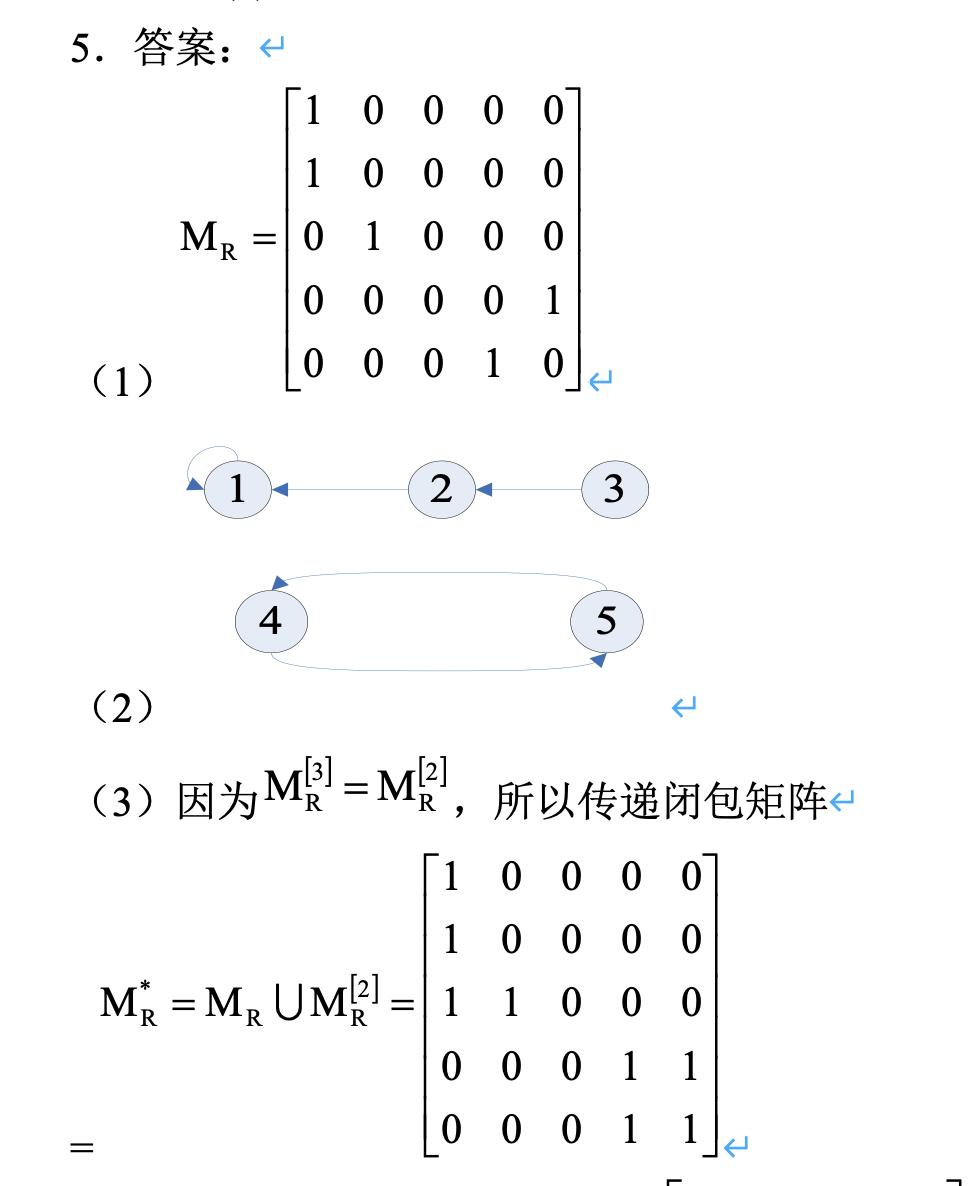
注意这里的4、5两个相互有通路,计算传递闭包的应该有(5,5)(4,4)
等价类
等价类是指在等价关系下,同一个等价类中的元素是等价的。在等价关系 R 下,给定一个元素 a∈A,其等价类 [a]R 是与 a 等价的所有元素的集合。形式上,[a]R={x∈A∣(a,x)∈R}。
我们来看一下题目中的具体等价关系 R:
集合 A={a,b,c,d,e,f},等价关系 R 为:
R={(a,a),(b,b),(c,c),(a,b),(b,a),(a,c),(c,a),(b,c),(c,b),(d,d),(e,e),(d,e),(e,d),(f,f)}
为了找到 [a]R,我们需要找出所有与 a 等价的元素。根据 R 的定义,我们可以看到:
(a,a),(a,b),(a,c),(b,a),(c,a)
所以,和 a 等价的元素有:a、b、c。
因此,[a]R={a,b,c}。
总结一下:
[a]R={a,b,c}
欧拉图、哈密顿图