大学物理(上)
力学
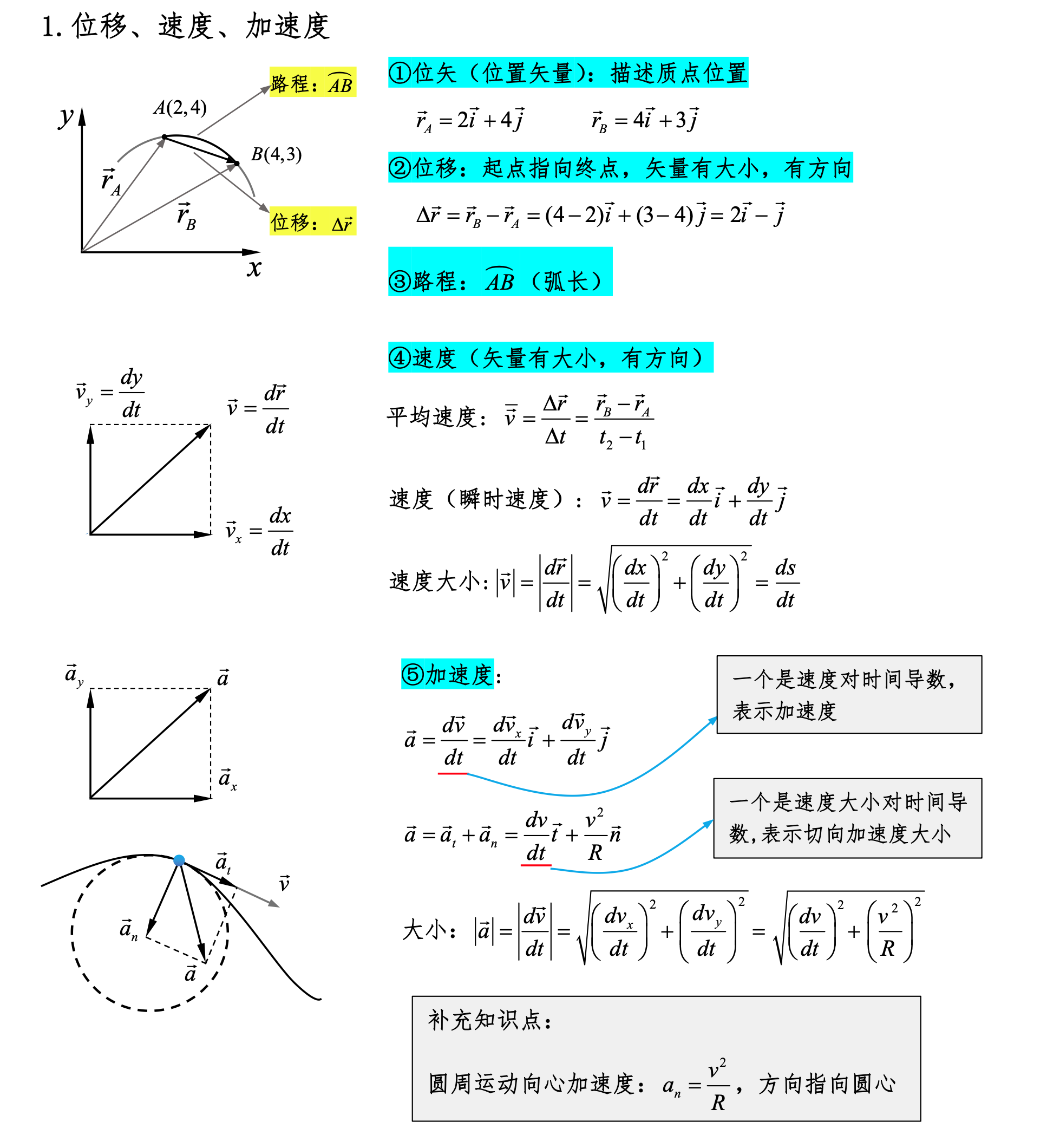
位移、速度、加速度
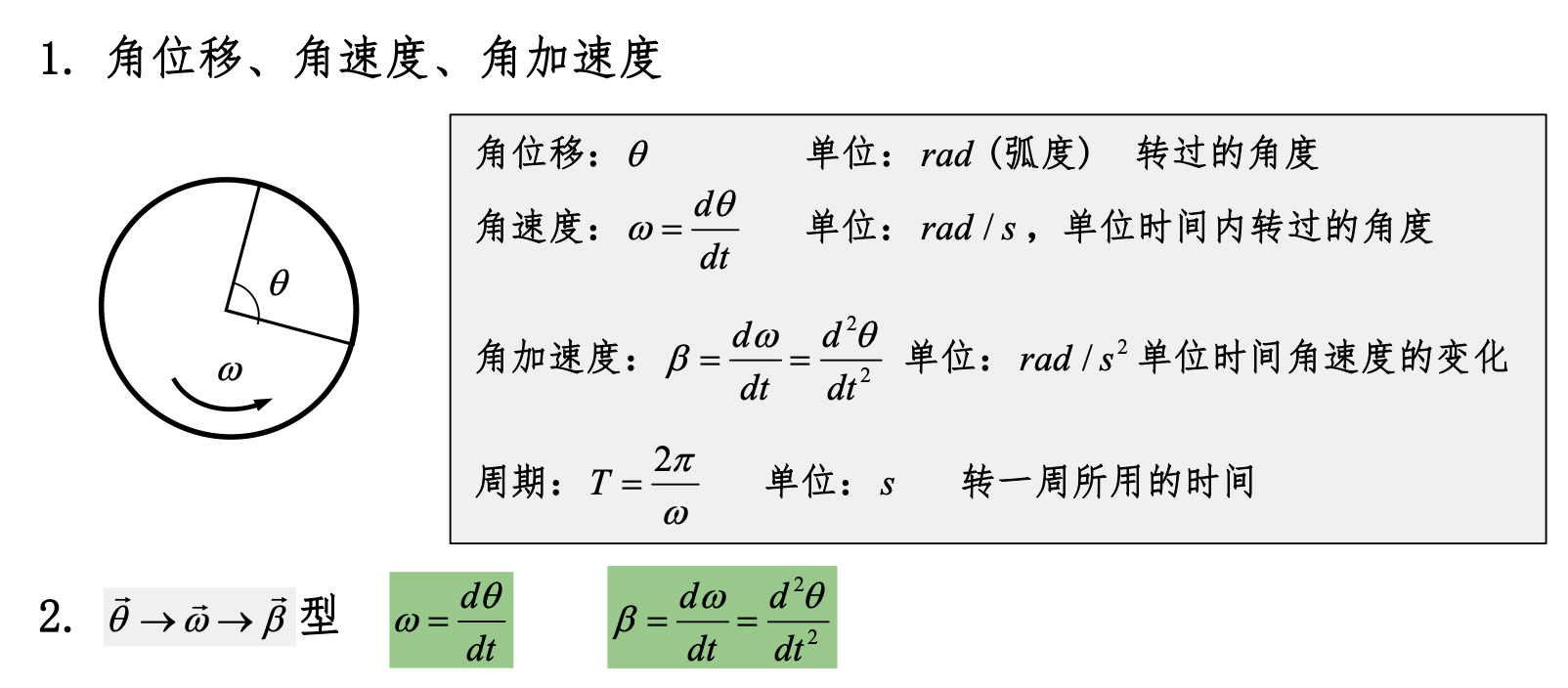
角位移、角速度、角加速度
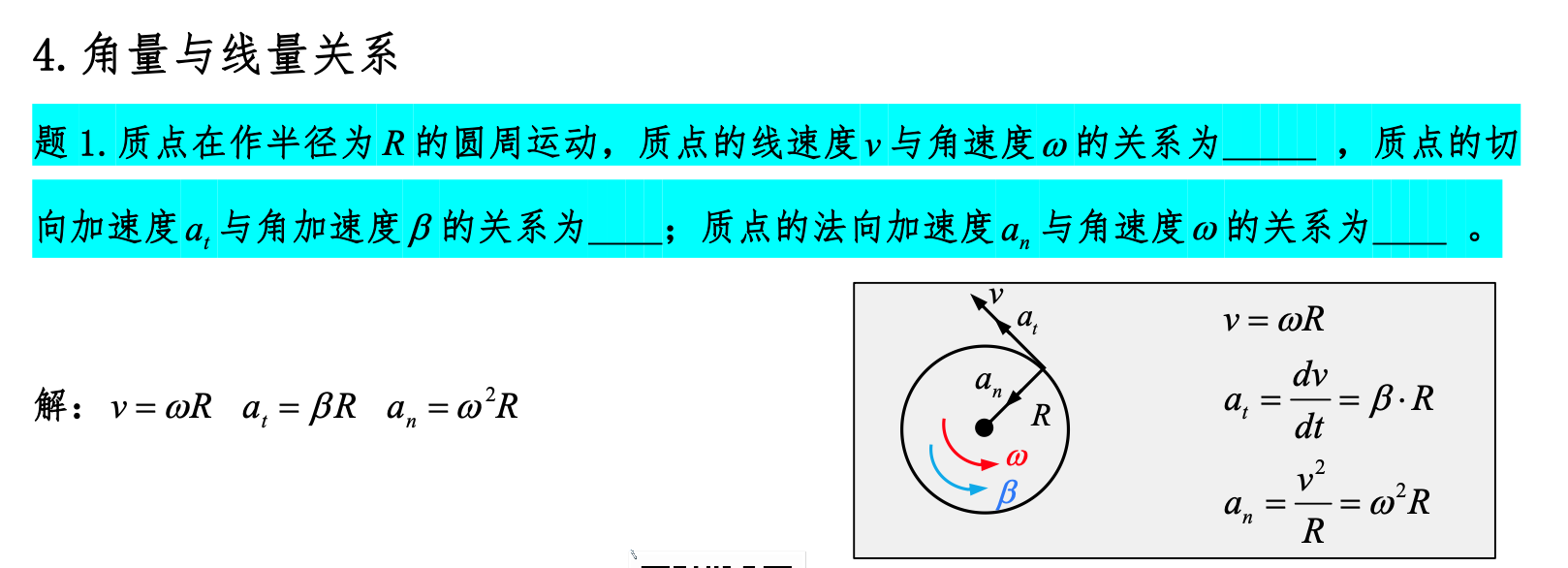
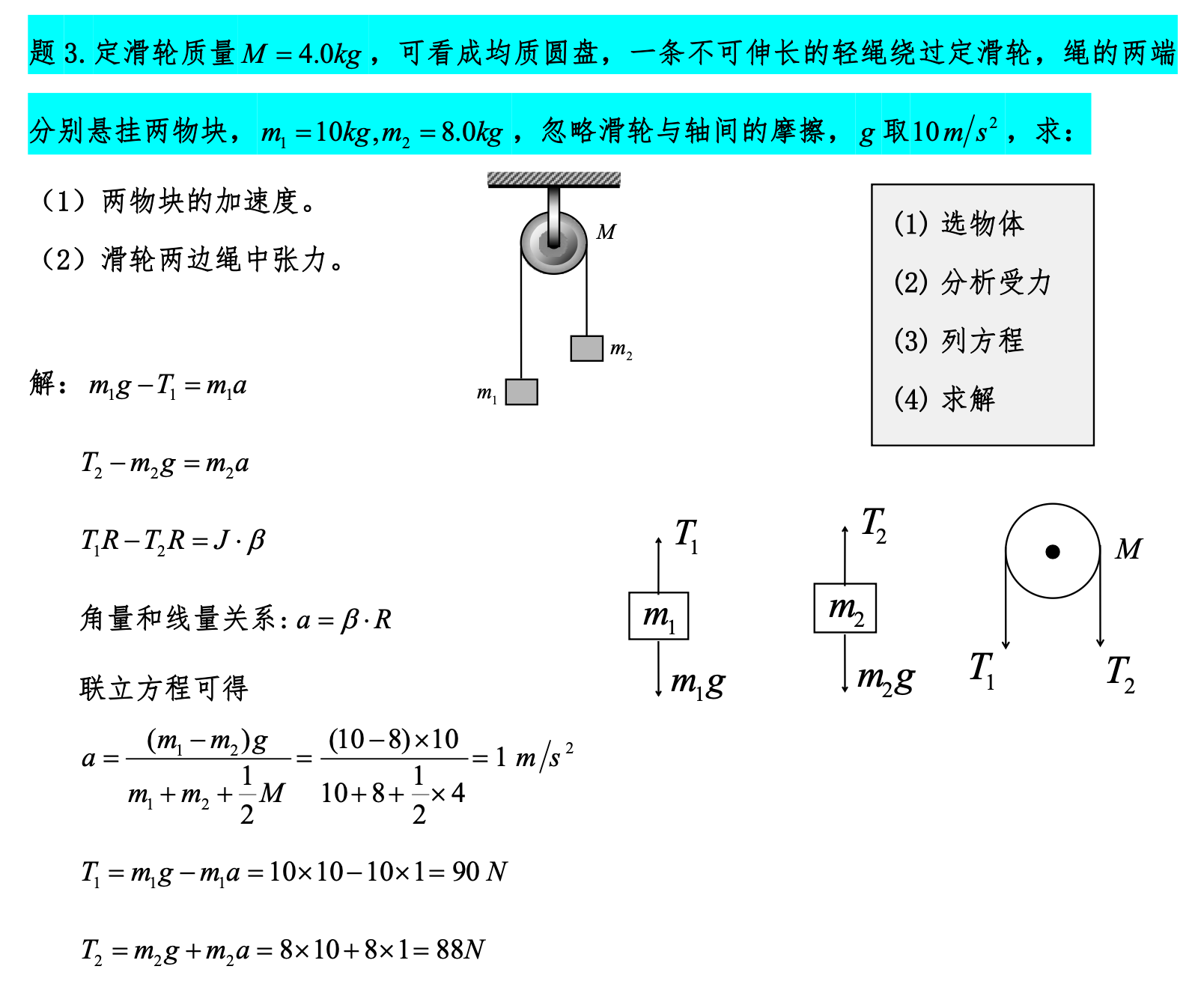
滑轮吊物块模型
牛顿第三定律
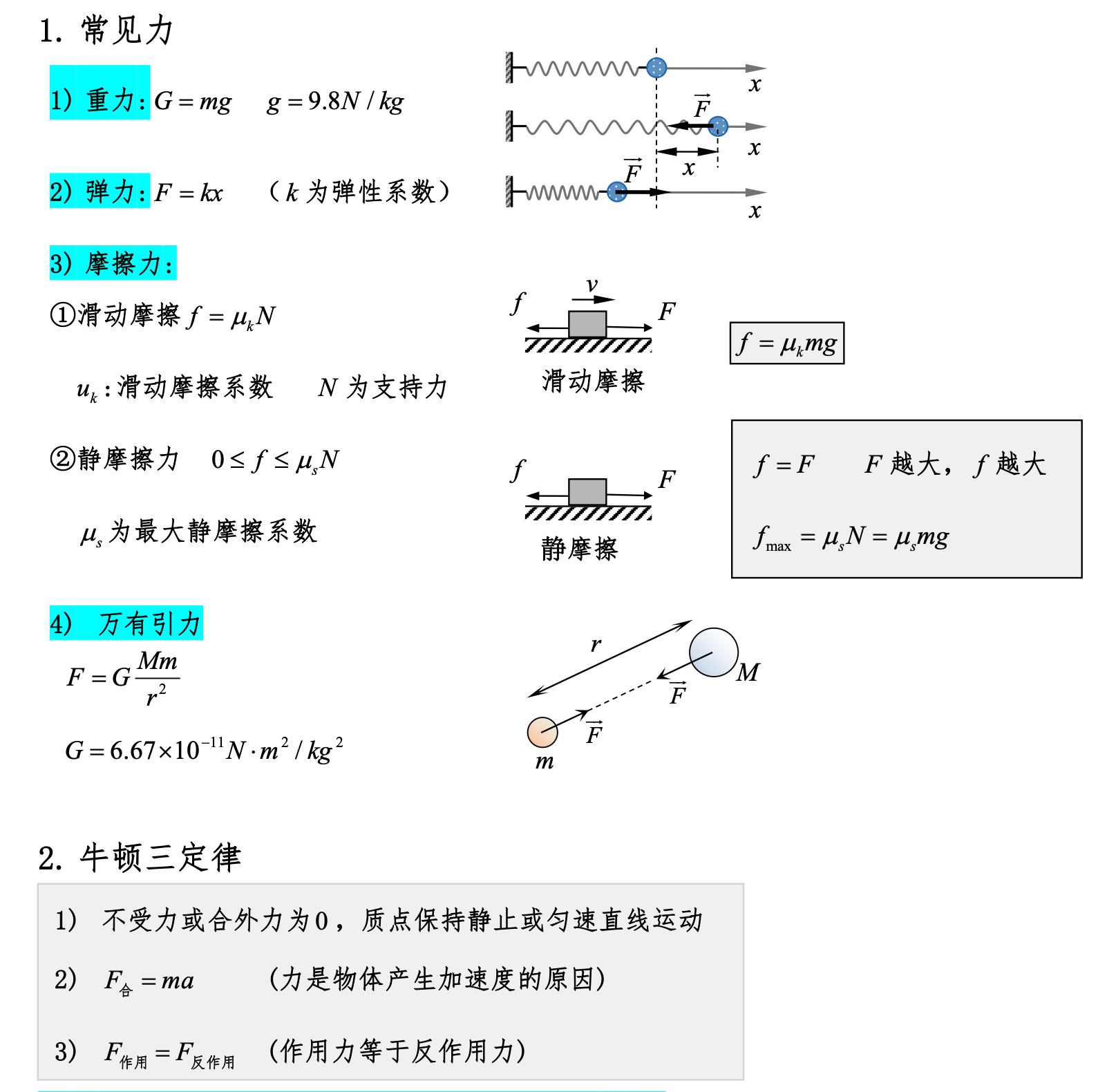
动量定理、动能定理


保守力、势能
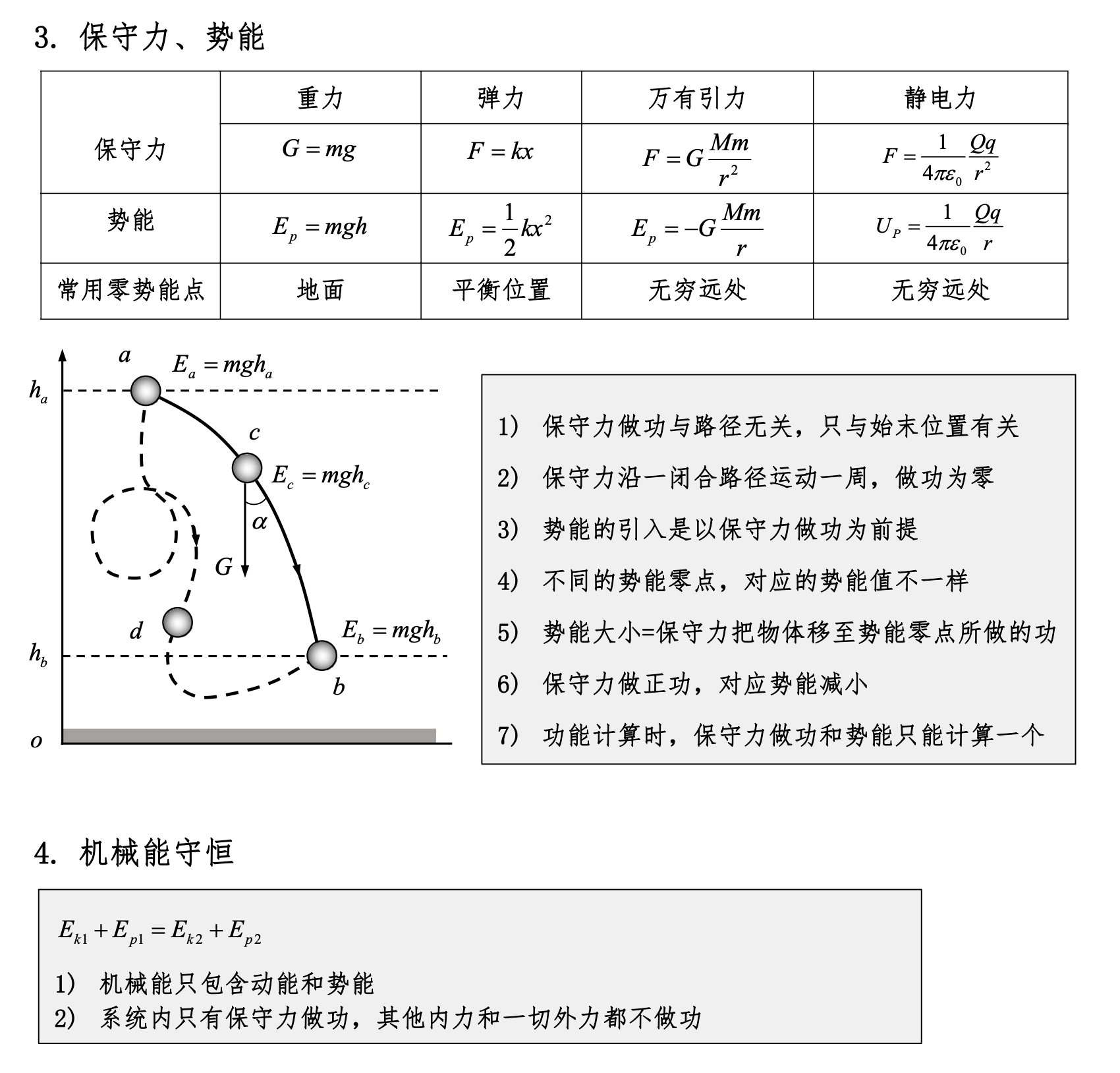
机械能守恒的条件
系统内只有保守力做功
机械能守恒是指系统的总机械能(动能和势能的总和)在某些条件下保持不变。具体条件如下:
- 系统内只有保守力做功:保守力是指其做功只与初末位置有关,与路径无关的力,如重力、弹力等。如果系统内只有保守力做功,机械能守恒。
- 没有非保守力(如摩擦力、空气阻力等)做功:非保守力做功会导致能量以热能或其他形式散失,使机械能不再守恒。
- 系统是封闭的:系统不与外界交换能量。
注意有摩擦力做功的系统机械能不守恒
动量守恒的条件
系统不受外力作用(或外力的合力为零)
动量守恒是指系统的总动量在某些条件下保持不变。具体条件如下:
- 系统内外力和内力的合力为零:如果系统不受外力作用(或外力的合力为零),系统的总动量守恒。
- 系统是封闭的:系统不与外界交换动量。
- 内力遵循牛顿第三定律:系统内各部分之间的相互作用力和反作用力大小相等,方向相反。
总结来说:
- 机械能守恒:系统内只有保守力做功,且没有能量以其他形式散失。
- 动量守恒:系统不受外力作用(或外力的合力为零),且系统是封闭的。
这两个定律在物理学中有广泛的应用,分别适用于不同的物理过程和系统。
变力做功
变力做功用积分
注意如果力是在几个纬度上的就分别计算每个维度上的力和位移的乘积最后再加起来**

转动惯量

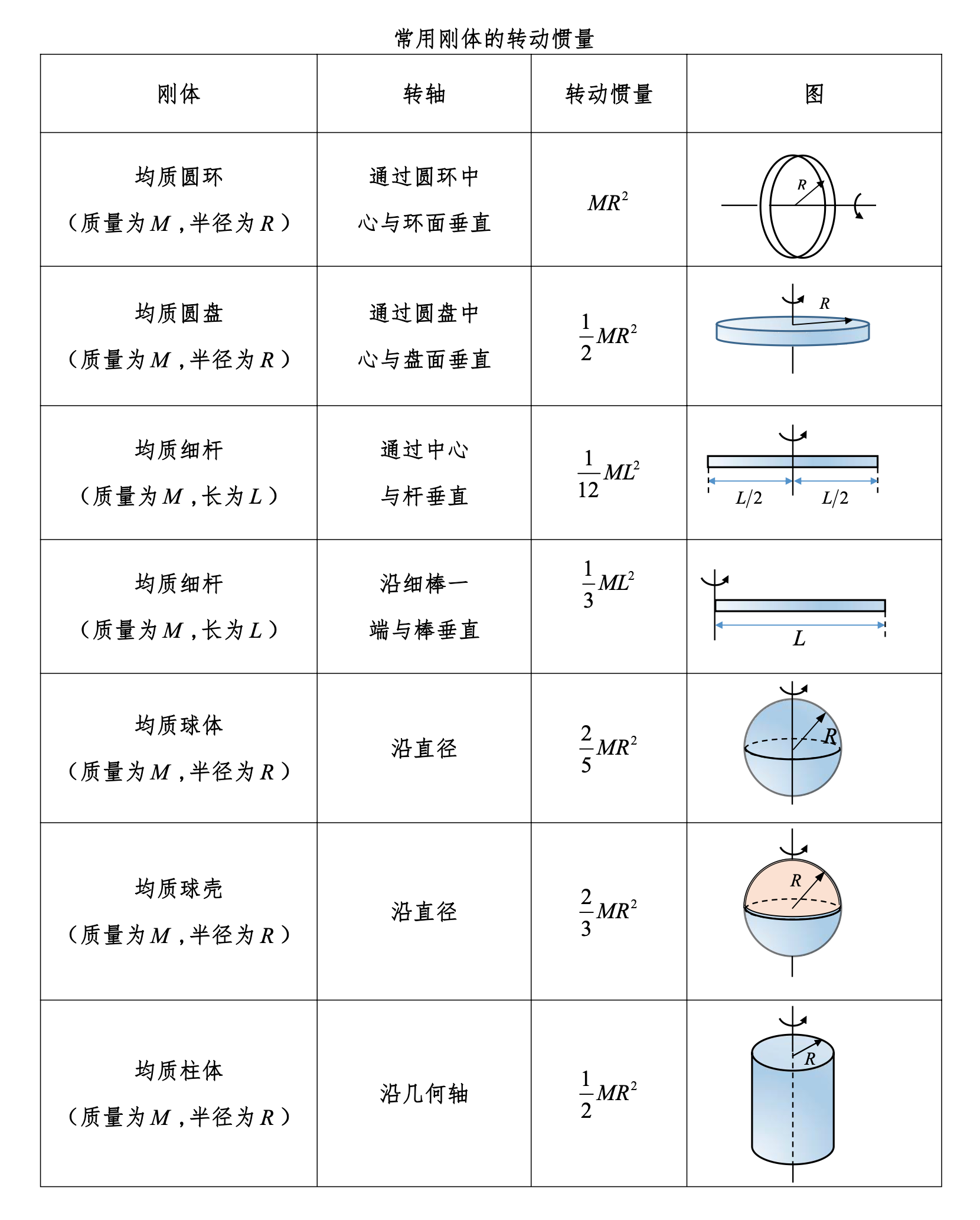
力矩
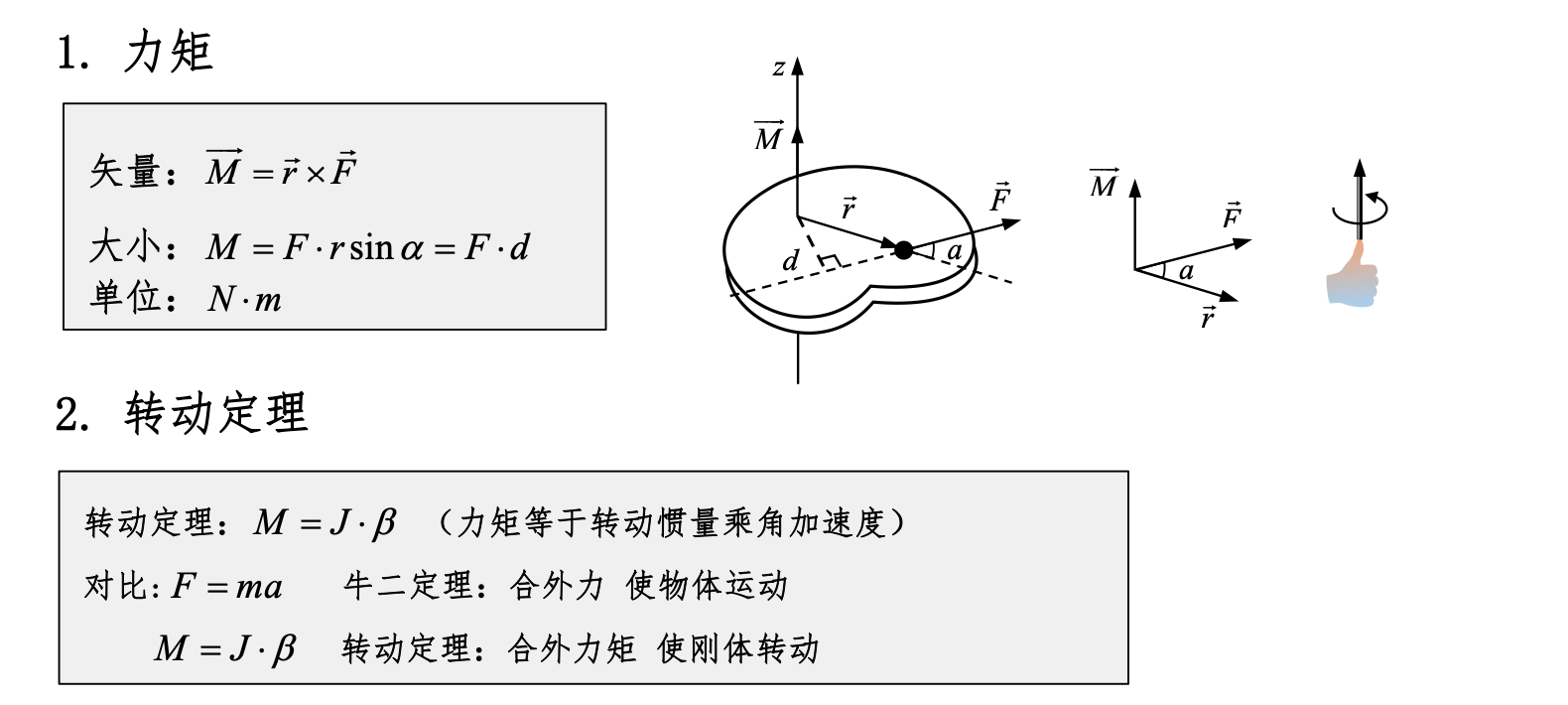
角动量
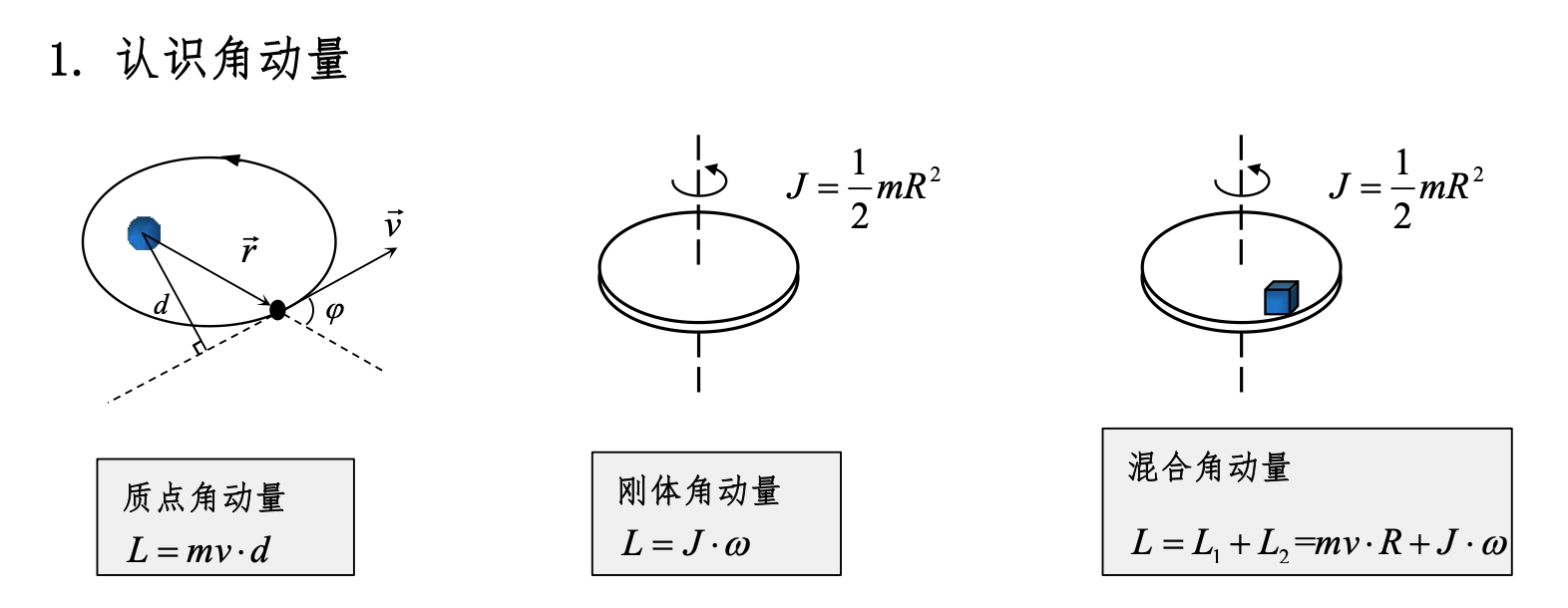
角动量守恒的条件
-
系统不受外力矩作用(合外力拒等于0):如果系统不受外力矩(或外力矩的合力为零),那么系统的总角动量守恒。外力矩是指作用在系统上的外力相对于某一固定点或轴的力矩。
-
系统是封闭的:系统不与外界交换�角动量,即没有外部物体对系统施加力矩。
-
内力矩的合力为零:系统内部的力矩相互抵消。根据牛顿第三定律,内力矩之间的作用和反作用力矩相等且方向相反,因此它们的合力为零。
-
角动量守恒的应用
-
天体运动:例如,行星绕恒星的轨道运动,如果忽略其他天体的影响,行星的角动量守恒。
-
旋转物体:例如,花样滑冰运动员在旋转时通过改变手臂和腿的位置来调整转速,这是因为她的角动量守恒。
-
粒子物理:在粒子碰撞和衰变过程中,角动量守恒是一个重要的约束条件。
刚体转动的功与能
力矩做功
力矩(或称扭矩)是使物体发生转动的力的效果。对于一刚体,力矩的定义为力的大小与力臂(力的作用点到转动轴的垂直距离)的乘积。数学上,力矩 可以表示为: 其中 是力臂, 是力的大小。
当力矩作用在刚体上并使其转动时,力矩做功。力矩做功的表达式为: 其中 是功, 是恒定力矩, 是转动的角度(弧度)。
刚体转动的动能定理
刚体的转动动能是由于其绕固定轴转动而产生的动能。刚体的转动动能 可以表示为: 其中 是刚体关于转动轴的转动惯量, 是角速度。
动能定理表明,刚体所受外力矩所做的总功等于刚体动能的变化。对于转动的刚体,动能定理可以表示为: 其中 是转动动能的变化, 是净力矩做的功。
刚体机械能守恒
在没有非保守力(如摩擦力)��作用时,刚体的机械能是守恒的。机械能包括动能和势能。对于刚体转动,机械能守恒定律可以表示为: 其中:
- 是刚体的平动动能,
- 是刚体的转动动能,
- 是刚体的势能。
对于纯转动的情况,平动动能为零。因此,机械能守恒定律简化为:
刚体平动和转动的重要公式
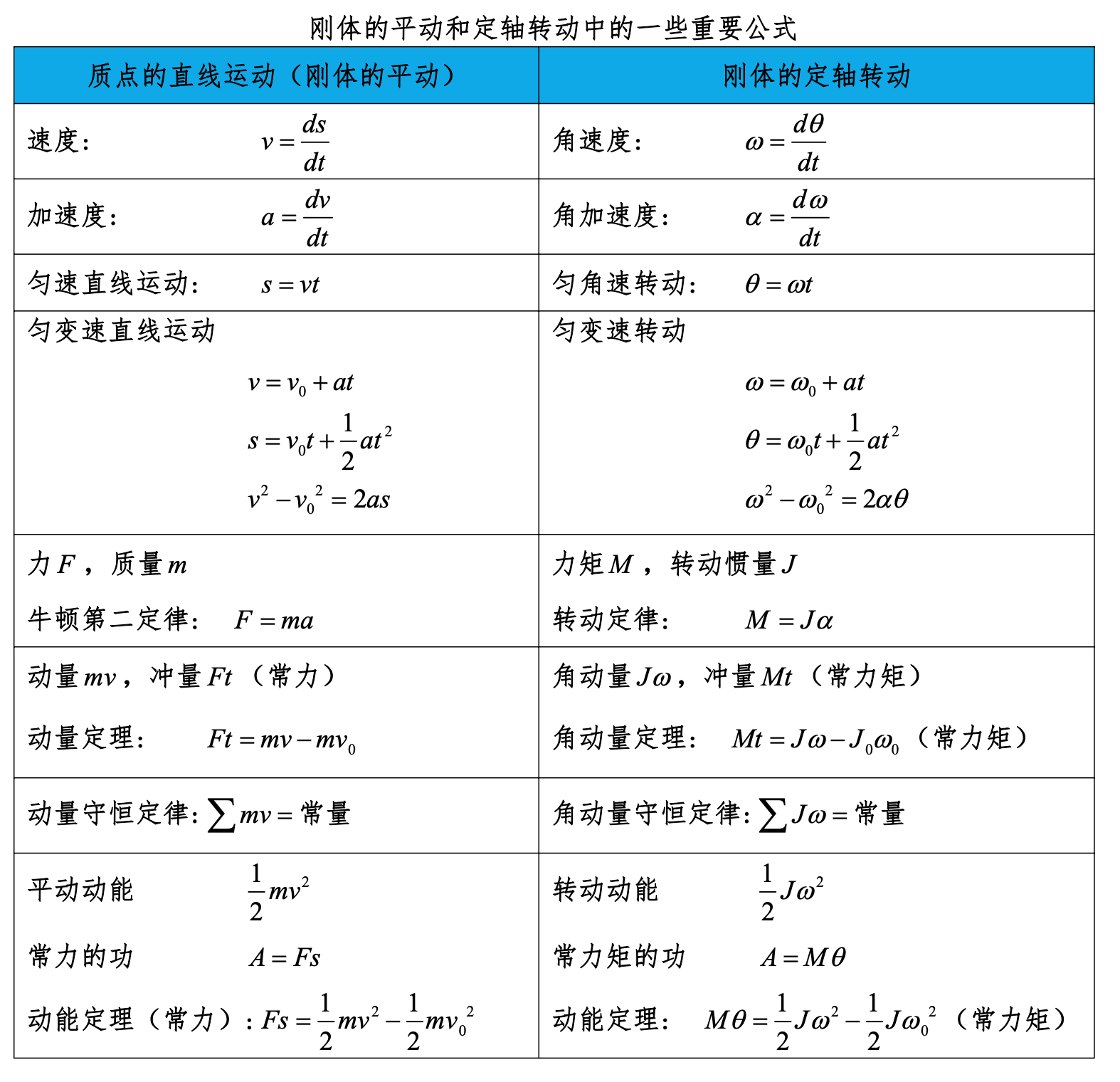
振动与波动
简谐运动
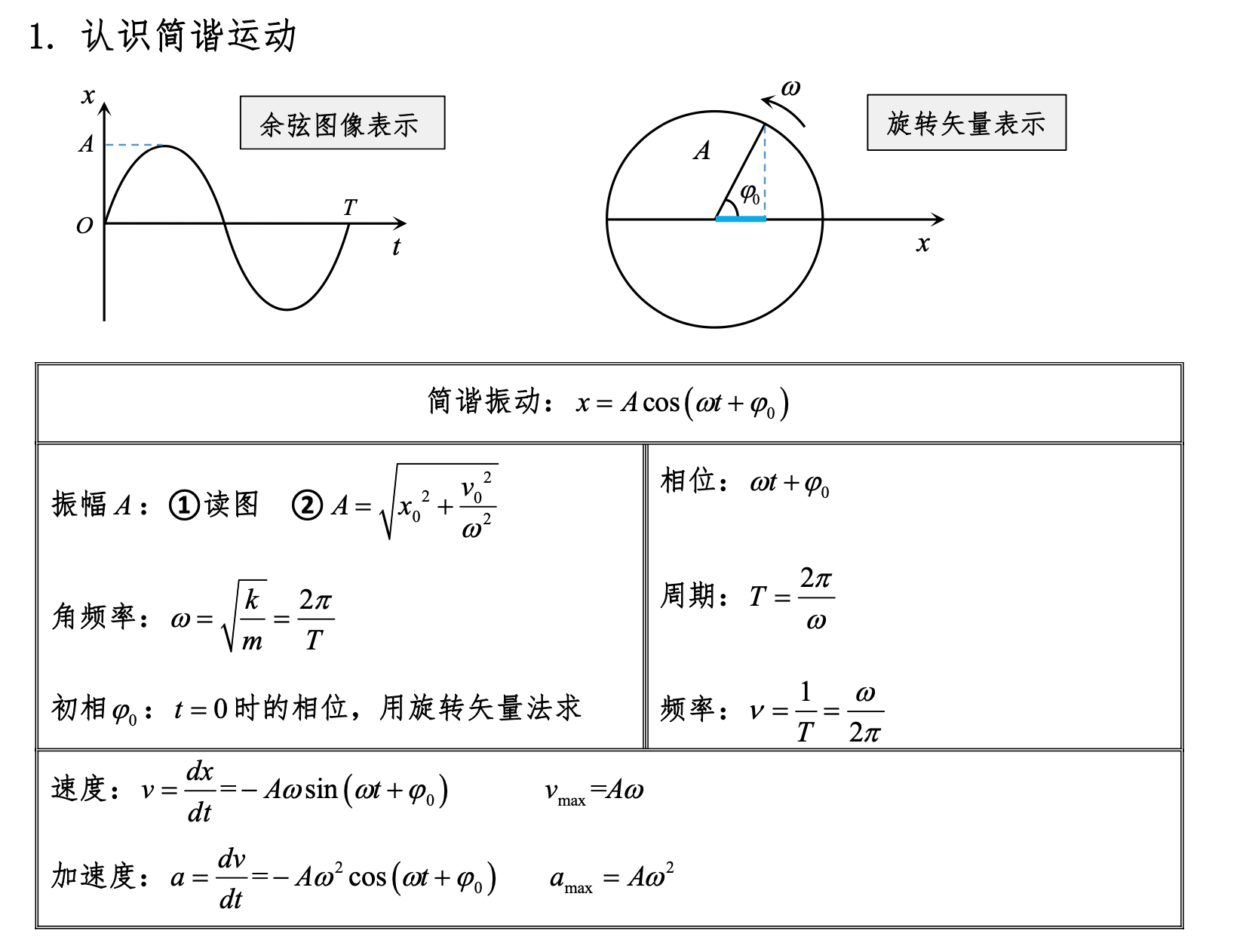
振动的合成

机械波、波动方程
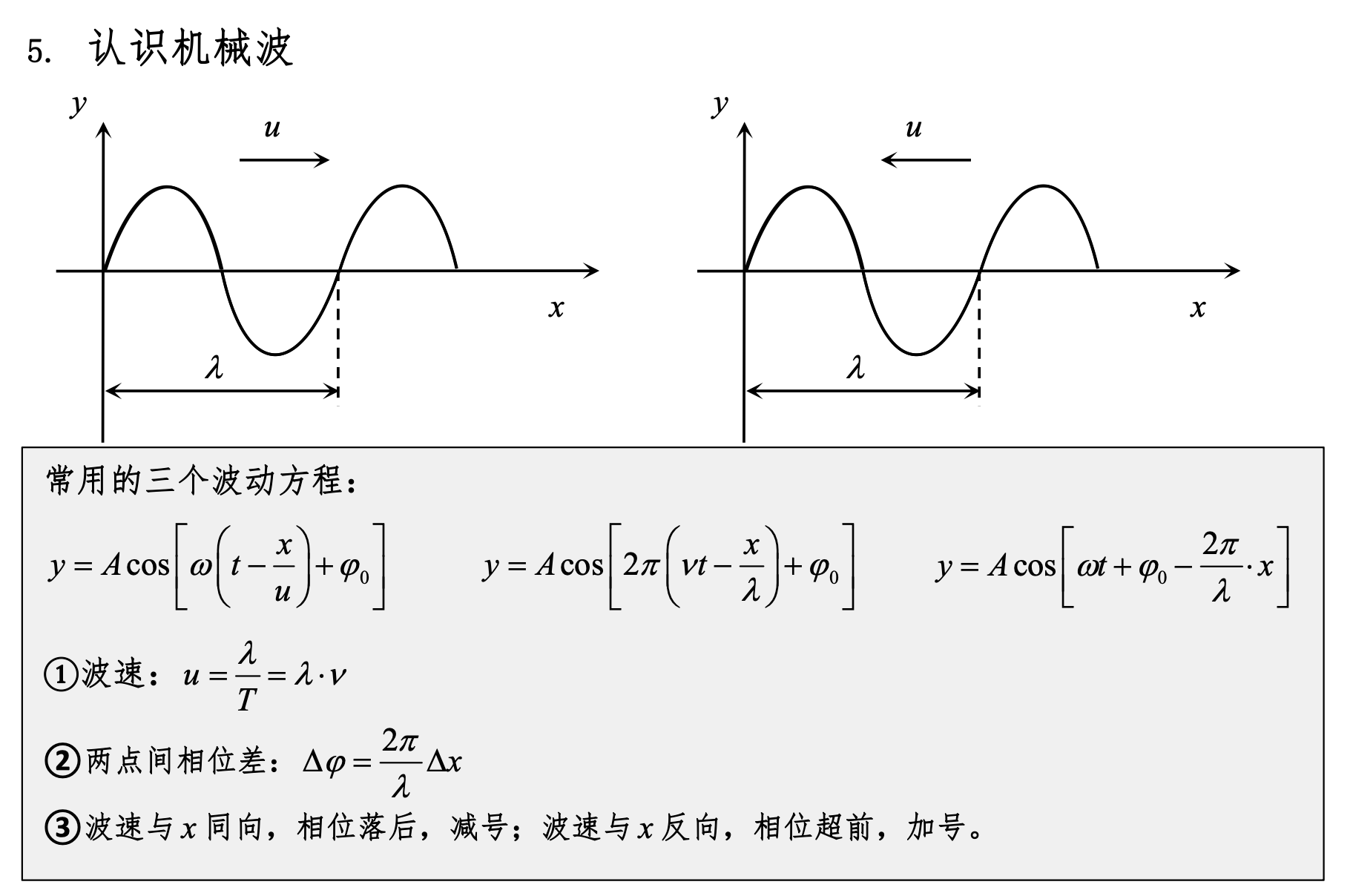
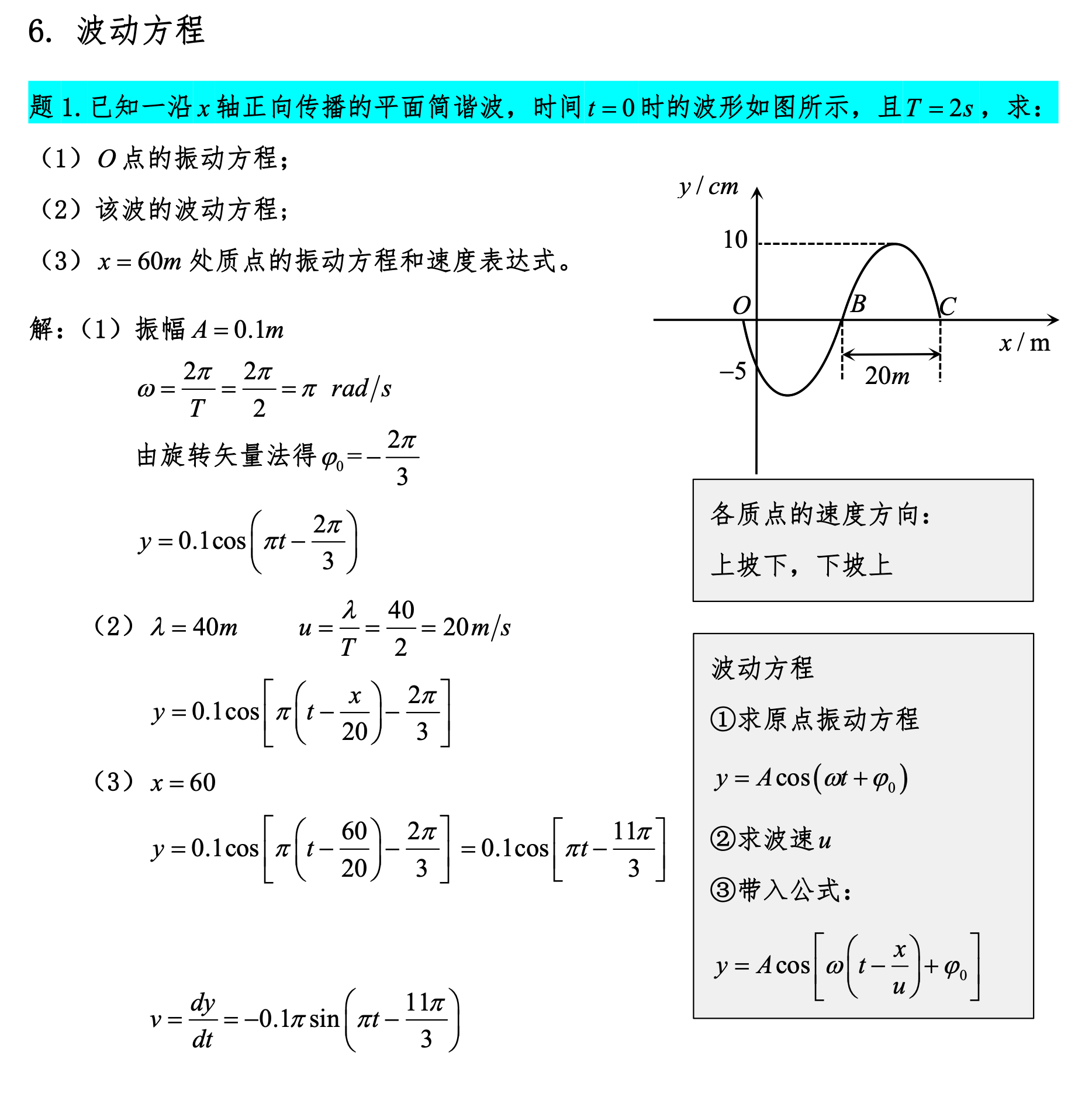
当然可以。大学物理中的波动部分涉及到波动现象及其能量传递的研究。下面是一些关于波动能量的关键知识点:
波的干涉
注意答案中的那个两个波在某一点的相位差公式


波动的能量
注意这里要跟单个质点振动区分开
-
能量传播:波动传递能量,而不是物质本身。
-
波动能量:可以分为动能和势能。动能来自介质的运动,势能来自介质的变形(如压缩或拉伸)。
-
振幅与能量:波的能量与振幅的平方成正比。即,振幅越大,波携带的能量越多。
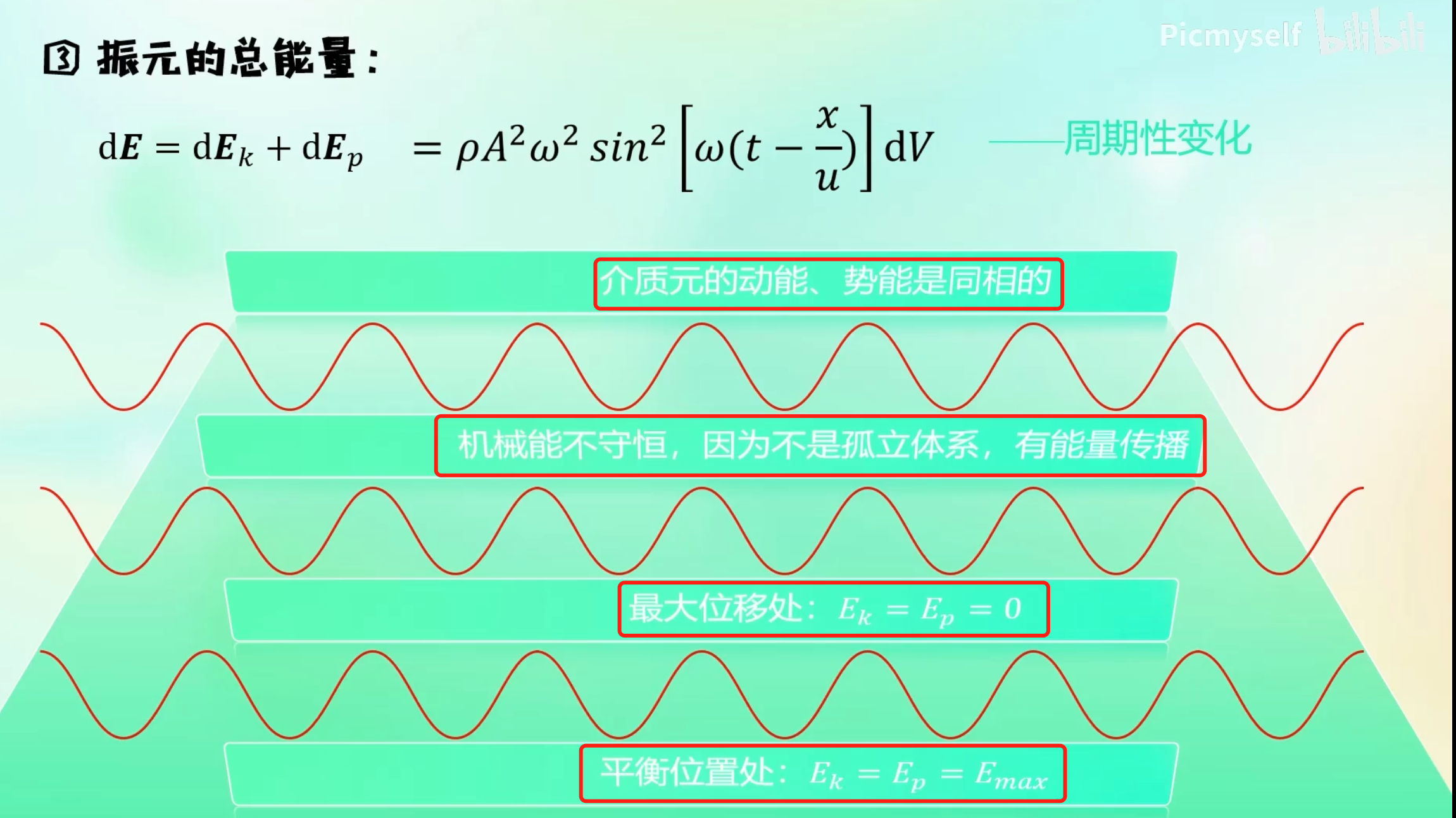
波动振元能量的四个结论:注意这里是波动
- 振元的动能和势能是相等的
- 振元的机械能不守恒,因为不是一独立的体系,波动会传递能量
- 位移最大处:动能和势能都为0
- 平衡位置处:动能和势能都最大
详细解读请看视频机械波的能量
光学
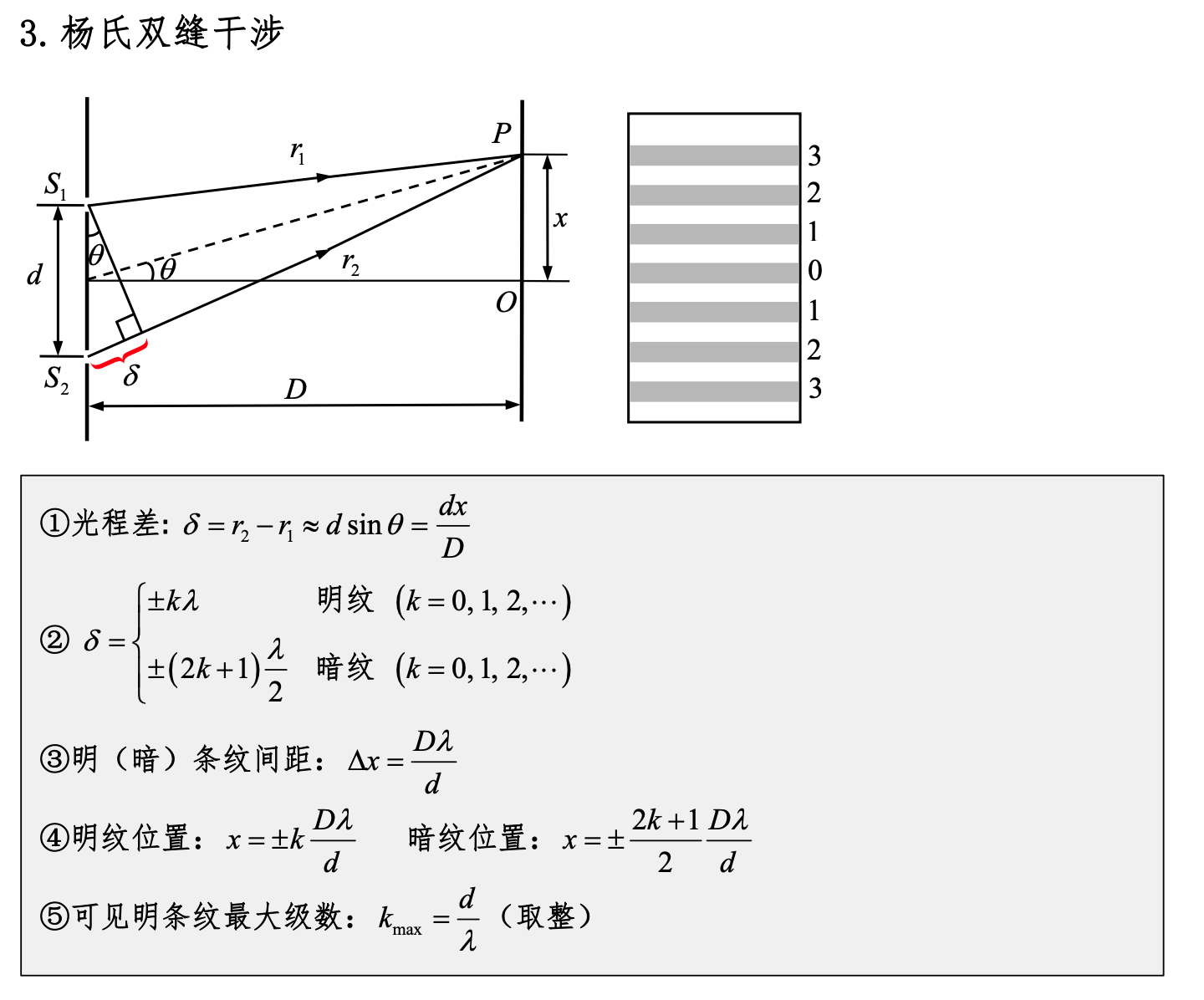
双缝干涉
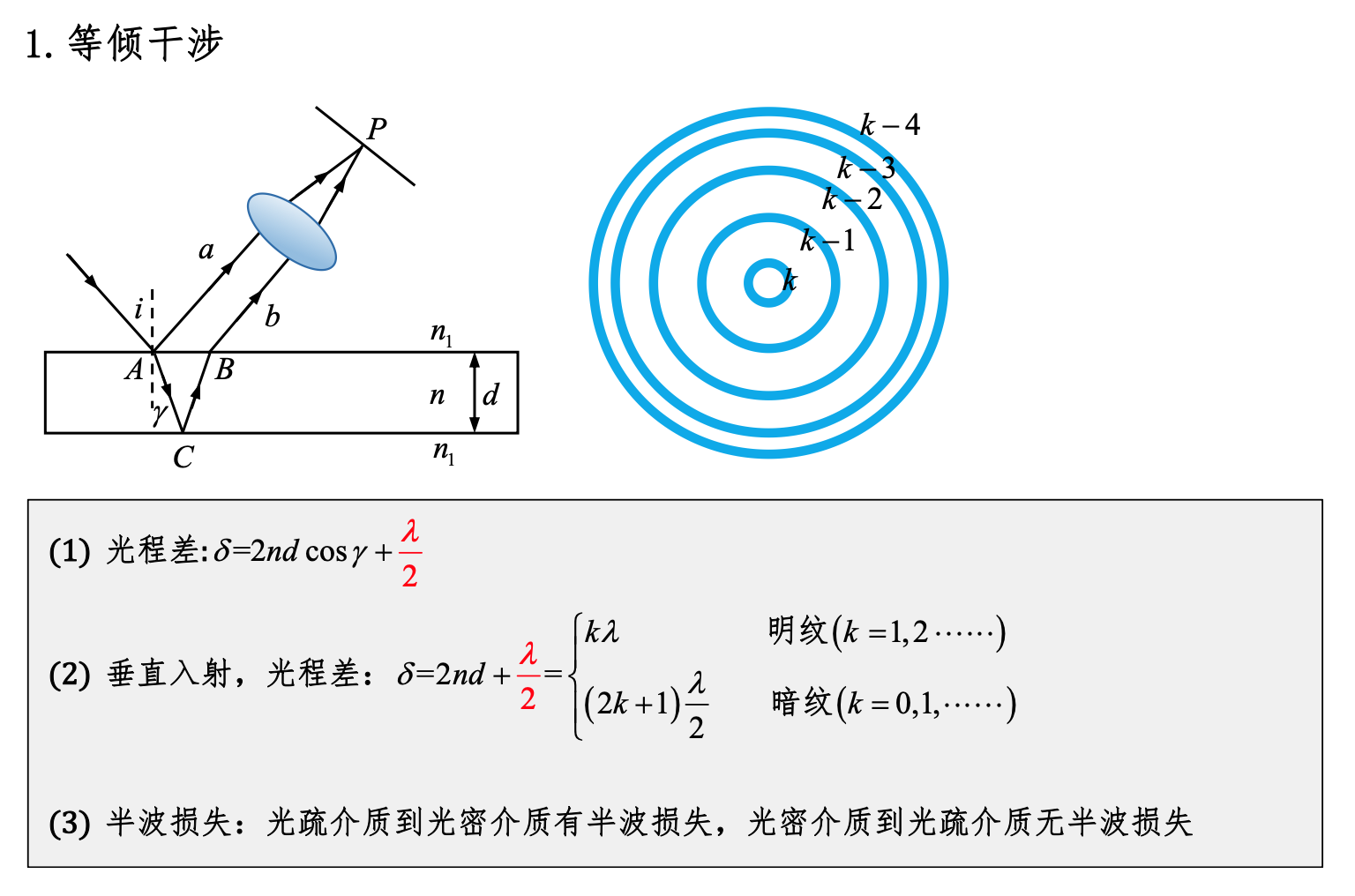
等倾干涉、半波损失
劈尖干涉
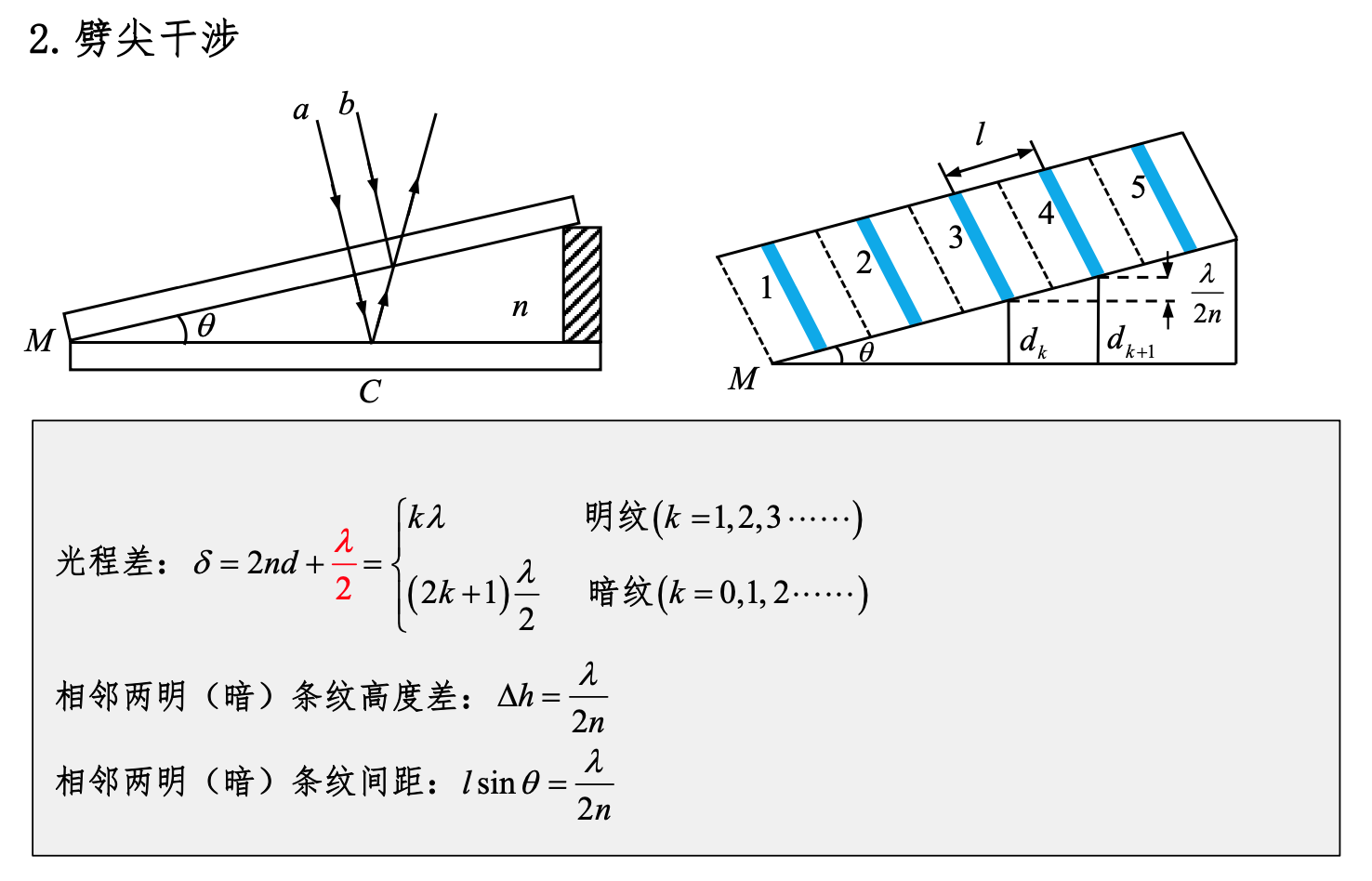
牛顿环
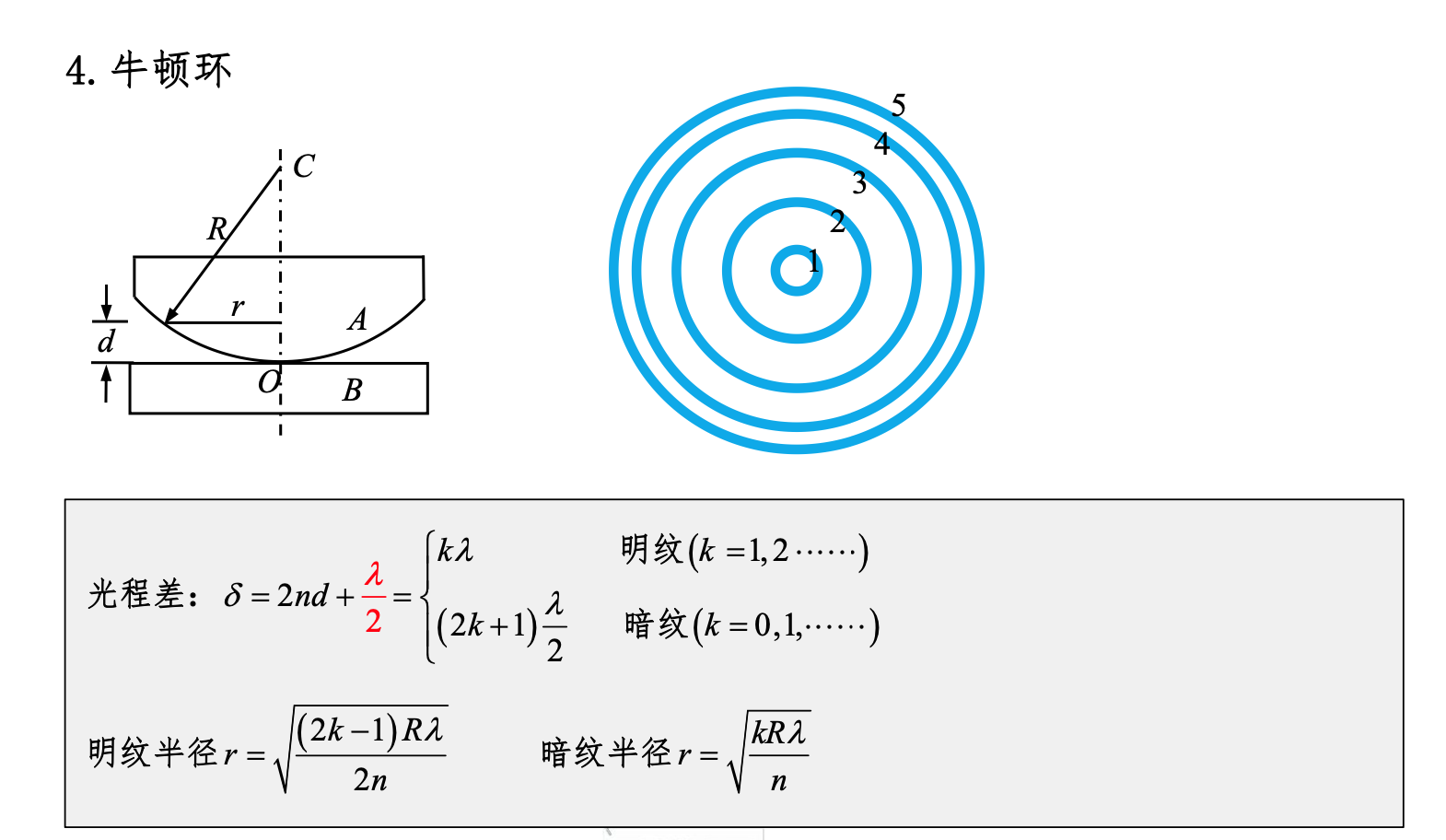
单缝衍射
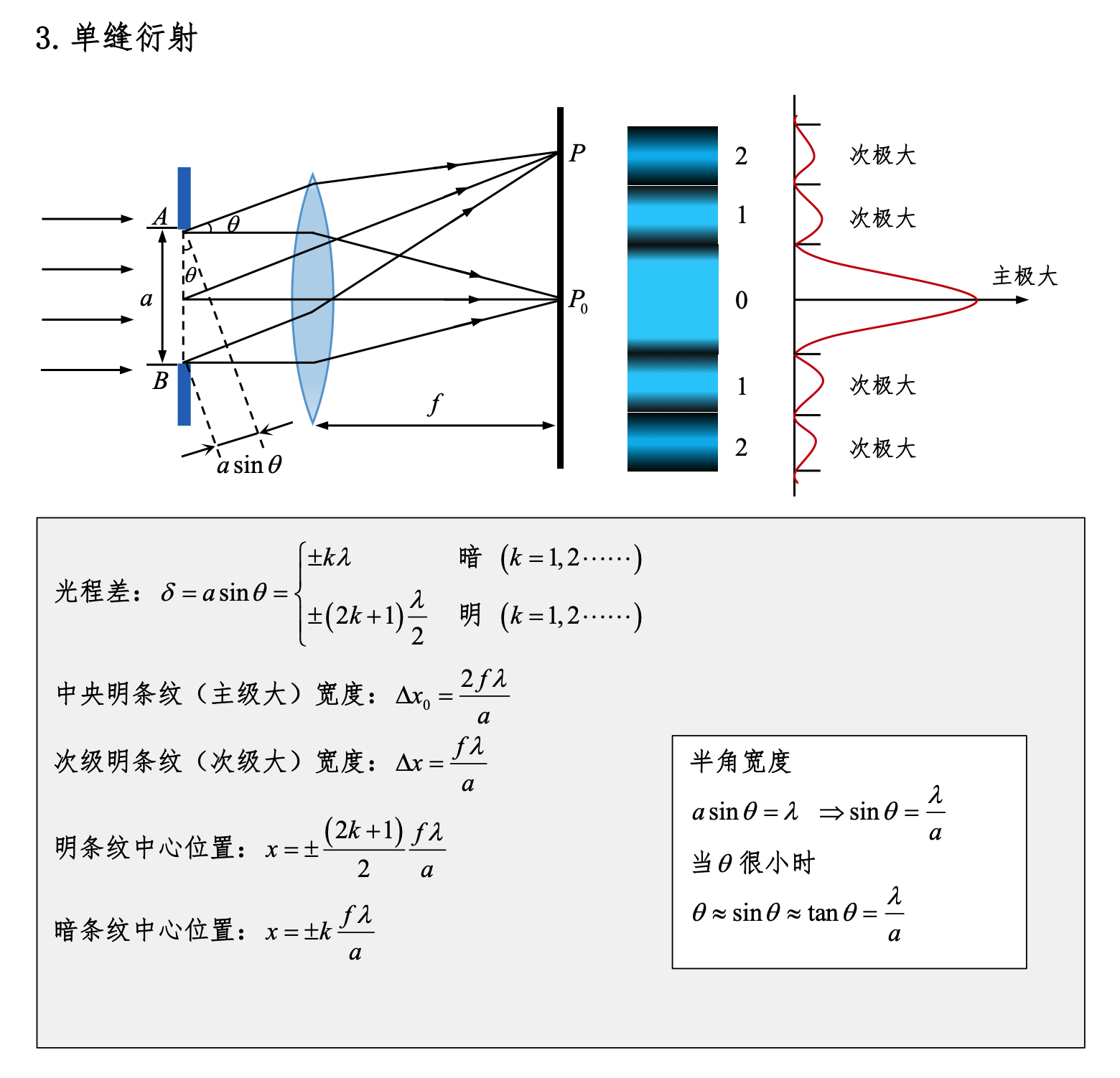
光栅衍射
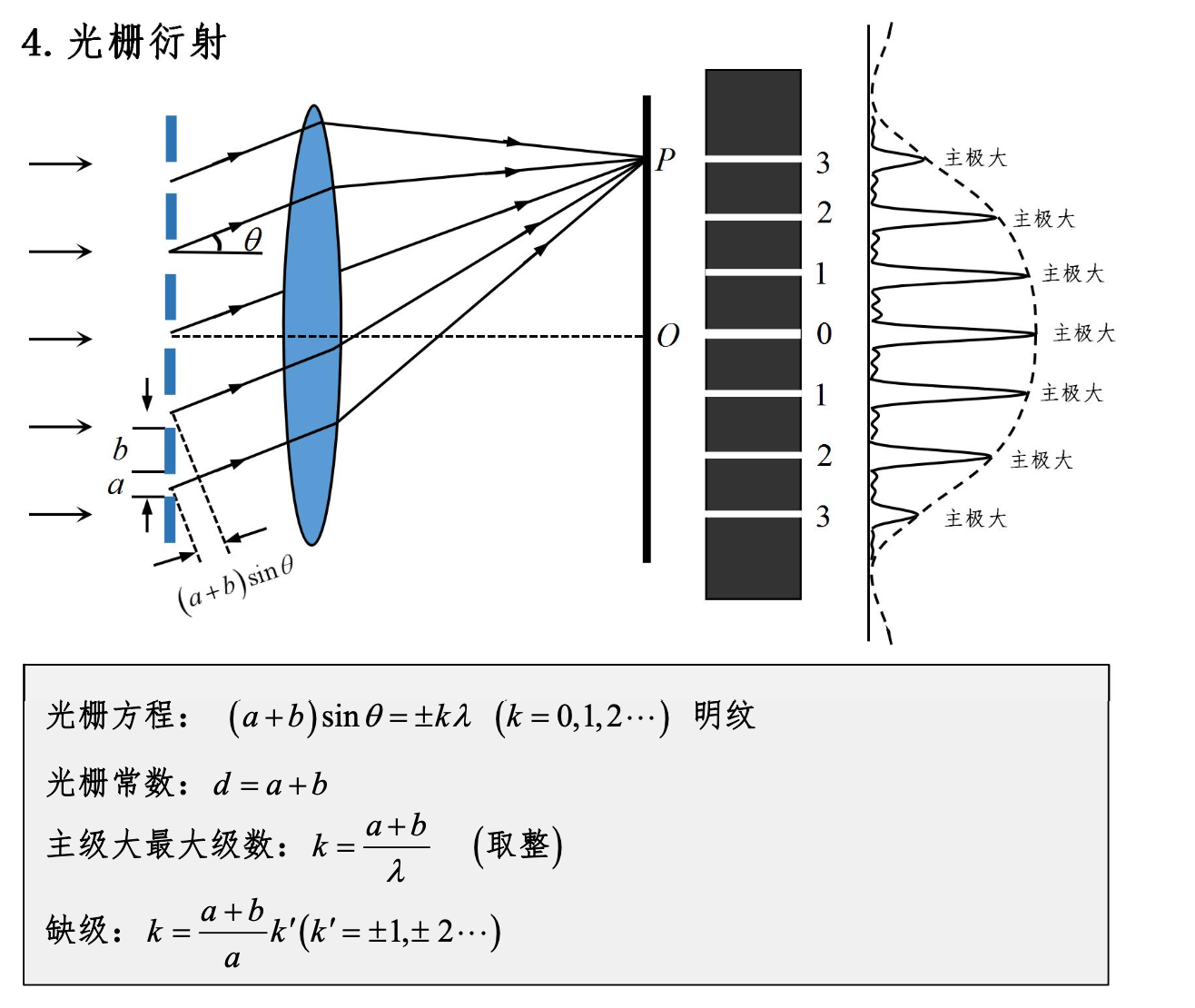
光栅常数的单位是长度单位,通常以米(m)、毫米(mm)、微米(µm)或纳米(nm)来表示。
光栅常数
光栅常数(grating constant)定义为光栅上相邻两个狭缝或刻线之间的距离,也称为光栅周期(grating period)。
常用单位
- 米(m):适用于非常大的光栅周期。
- 毫米(mm):常用于一般光栅。
- 微米(µm):非常常见的单位,因为光栅周期通常在这个范围。
- 纳米(nm):适用于非常精细的光栅。
例子
- 对于一个常见的光栅,如果每毫米有1000条刻线,那么光栅常数就是1微米(µm)。
- 对于更细致的光栅,如果每毫米有10,000条刻线,那么光栅常数就是100纳米(nm)。
总结
光栅常数通常用米(m)、毫米(mm)、微米(µm)或纳米(nm)来表示,选择哪个单位取决于光栅的具体尺寸和应用。
长度单位换算
-
米(m)
- 1 m = 100 cm
- 1 m = 1,000 mm
- 1 m = (10^9) nm
- 1 m = (10^6) µm
- 1 m = (10^12) pm
- 1 m = (10^10) Å
-
厘米(cm)
- 1 cm = 0.01 m
- 1 cm = 10 mm
- 1 cm = (10^7) nm
- 1 cm = (10^4) µm
- 1 cm = (10^10) pm
- 1 cm = (10^8) Å
-
毫米(mm)
- 1 mm = 0.1 cm
- 1 mm = (10^-3) m
- 1 mm = (10^6) nm
- 1 mm = (10^3) µm
- 1 mm = (10^9) pm
- 1 mm = (10^7) Å
-
微米(µm)
- 1 µm = (10^-6) m
- 1 µm = (10^-4) cm
- 1 µm = 1,000 nm
- 1 µm = (10^6) pm
- 1 µm = (10^4) Å
-
纳米(nm)
- 1 nm = (10^-9) m
- 1 nm = (10^-7) cm
- 1 nm = (10^-3) µm
- 1 nm = 1,000 pm
- 1 nm = 10 Å
-
埃(Å)
- 1 Å = (10^-10) m
- 1 Å = (10^-8) cm
- 1 Å = (10^-4) µm
- 1 Å = 0.1 nm
- 1 Å = 100 pm
-
皮米(pm)
- 1 pm = (10^-12) m
- 1 pm = (10^-10) cm
- 1 pm = (10^-6) µm
- 1 pm = (10^-3) nm
- 1 pm = 0.01 Å
- 1 米 (m) = 100 厘米 (cm) = 1,000 毫米 (mm) = (10^6) 微米 (µm) = (10^9) 纳米 (nm) = (10^10) 埃 (Å) = (10^12) 皮米 (pm)
- 1 厘米 (cm) = 0.01 米 (m) = 10 毫米 (mm) = (10^4) 微米 (µm) = (10^7) 纳米 (nm) = (10^8) 埃 (Å) = (10^10) 皮米 (pm)
- 1 毫米 (mm) = 0.1 厘米 (cm) = 0.001 米 (m) = (10^3) 微米 (µm) = (10^6) 纳米 (nm) = (10^7) 埃 (Å) = (10^9) 皮米 (pm)
- 1 微米 (µm) = (10^-6) 米 (m) = (10^-4) 厘米 (cm) = (10^-3) 毫米 (mm) = (10^3) 纳米 (nm) = (10^4) 埃 (Å) = (10^6) 皮米 (pm)
- 1 纳米 (nm) = (10^-9) 米 (m) = (10^-7) 厘米 (cm) = (10^-6) 毫米 (mm) = (10^-3) 微米 (µm) = 10 埃 (Å) = 1,000 皮米 (pm)
- 1 埃 (Å) = (10^-10) 米 (m) = (10^-8) 厘米 (cm) = (10^-7) 毫米 (mm) = (10^-4) 微米 (µm) = 0.1 纳米 (nm) = 100 皮米 (pm)
- 1 皮米 (pm) = (10^-12) 米 (m) = (10^-10) 厘米 (cm) = (10^-9) 毫米 (mm) = (10^-6) 微米 (µm) = (10^-3) 纳米 (nm) = 0.01 埃 (Å)
第六周简答题
第七周简答题
- 机械波与机械振动的关系
机械振动是指物体或质点在平衡位置附近的往复运动。机械波则是机械振动在介质中的传播。具体来说,当一个质点在介质中振动时,它会通过相互作用将振动传递给相邻的质点,从而形成波动。这种传播过程就是机械波。因此,机械波可以看作是机械振动在介质中的传递。
- 机械波形成的条件
机械波的形成需要以下几个条件:
- 介质:机械波需要通过介质传播,介质可以是固体、液体或气体。
- 振动源:需要有一个振动源来产生初始的机械振动。
- 介质的弹性和惯性:介质必须具有弹性(即介质中的质点能够相互作用)和惯性(即质点具有质量)。
- 波的分类
波可以根据不同的标准进行分类:
- 按波的传播方向和质点振动方向的关系:
- 纵波:质点的振动方向与波的传播方向平行(如声波)。
- 横波:质点的振动方向与波的传播方向垂直(如水波、光波)。
- 按波的传播介质:
- 机械波:需要介质传播(如声波、水波)。
- 电磁波:不需要介质也能传播(如光波、无线电波)。
- 按波的形状:
- 平面波:波面是平面。
- 球面波:波面是球面。
- 按波的性质:
- 简谐波:波形为正弦或余弦函数。
- 非简谐波:波形为复杂的非正弦函数。
- 描述波的物理量
描述波的物理量主要有以下几个:
- 波长 ((\lambda)):相邻两个波峰或波谷之间的距离。
- 频率 ((f)):单位时间内通过某点的波的周期数。
- 周期 ((T)):完成一次完整振动所需的时间,。
- 波速 ((v)):波在介质中传播的速度。
- 振幅 ((A)):波的最大位移。
- 相位 ((\phi)):描述波在某一时刻、某一位置的状态。
- 波动的能量特征
波动的能量具有以下特征:
- 能量传播:波动能量随波的传播方向传递。
- 能量与振幅的关系:波的能量与振幅的平方成正比。
- 能量密度:单位体积内波动的能量。
- 能量流密度:单位时间内通过单位面积的能量,通常称为波的强度。
-
什么叫平面简谐波 平面简谐波是指波面为平面的简谐波。它的波形可以用正弦或余弦函数来描述,且在空间中传播时,波的传播方向与波面垂直。平面简谐波的数学表达式通常为: [ y(x, t) = A \cos(kx - \omega t + \phi) ] 其中,(A) 是振幅,(k) 是波数,(\omega) 是角频率,(\phi) 是初相位。
-
平面简谐波的波形曲线中如何判断各质元的振动方向
在平面简谐波的波形曲线中,质元的振动方向可以通过波的相位变化来判断。具体步骤如下:
- 观察波形:确定波的传播方向(例如,波形 ( y(x, t) = A \cos(kx - \omega t + \phi) ) 中,波沿正 (x) 方向传播)。
- 相位变化:观察波形在某一点的相位随时间的变化。如果波形在某一点的相位增加(例如,(kx - \omega t + \phi) 中,随时间 (t) 增加,相位 (-\omega t) 减小),则该点的质元向负方向振动;相反,如果相位减小,则质元向正方向振动。
- 波形图像:在波形图像中,波峰和波谷的移动方向即为波的传播方向,而质元的振动方向与波传播方向的关系可以通过波形的正弦或余弦函数的导数来确定。例如,在波峰处,质元的速度为零,但加速度最大,指向平衡位置。
第八周简答题
好的,我们来详细讨论这些问题。
1. 什么是波的��传播独立性原理?
波的传播独立性原理: 波的传播独立性原理表明,当两束或多束波在空间中传播时,它们彼此独立传播,不会相互影响。这意味着每一束波会按照自己的传播路径和速度传播,而不受其他波的存在和传播方式的影响。这个原理在波动理论中是基础性的,适用于各种类型的波,如声波、光波和水波。
2. 什么是波的叠加原理?
波的叠加原理(Principle of Superposition): 波的叠加原理是指,当两束或多束波在空间中相遇时,总的波动是各个波动的代数和。具体来说,如果两束波在某一点的位移分别为 ( y_1 ) 和 ( y_2 ),那么它们在该点的总位移 ( y ) 为:
[ y = y_1 + y_2 ]
波的叠加原理适用于线性波动系统,是理解干涉和衍射现象的基础。
3. 波的相干条件是什么?
波的相干条件: 两束波要产生稳定的干涉图样,必须满足以下相干条件:
- 相同频率: 两束波必须具有相同的频率(或波长),以确保它们的相位差恒定。
- 恒定相位差: 两束波之间的相位差必须是恒定的,不能随时间变化。这通常意味着两束波必须来自同一光源或通过分光产生。
- 相同偏振状态: 两束波的偏振状态必须相同或固定,以确保它们可以有效地叠加。
4. 波的干涉和振动合成有什么联系?
波的干涉和振动合成的联系: 波的干涉是波的叠加原理在空间和时间上的表现。当两束相干波相遇时,它们的振动(位移)在相遇点叠加,形成新的振动模式。干涉现象可以看作是振动合成的结果,其中:
- 相长干涉(Constructive Interference): 当两束波的相位相同或相差为整数倍的 ( 2\pi ) 时,它们的振动在相遇点叠加,形成振幅更大的波。
- 相消干涉(Destructive Interference): 当两束波的相位相差为奇数倍的 ( \pi ) 时,它们的振动在相遇点相互抵消,形成振幅较小甚至为零的波。
5. 什么叫衍射?
衍射(Diffraction): 衍射是波遇到障碍物或通过狭缝时发生的绕射和弯曲现象。衍射使得波能够绕过障碍物传播,并在障碍物的阴影区中传播。衍射现象在光波、声波和水波中都可以观察到。
衍射的显著特征是:
- 当障碍物或狭缝的尺寸与波长相近时,衍射现象最明显。
- 衍射导致波在障碍物�后方形成干涉图样,表现为明暗相间的条纹或斑点。
6. 惠更斯原理内容?
惠更斯原理(Huygens' Principle): 惠更斯原理是解释波传播的一种方法。它的内容包括:
- 每个波前上的点都是新的子波源: 波前上的每一个点都可以看作是一个新的子波源,这些子波以相同的速度向外传播。
- 新的波前是子波的包络面: 在任意时刻,新的波前是所有这些子波的包络面,即所有子波的波面相切的曲面。
惠更斯原理可以用来解释各种波动现象,如反射、折射、衍射和干涉。特别是在衍射现象中,惠更斯原理帮助我们理解波如何绕过障碍物传播并形成复杂的干涉图样。
第九周简答题
1. 什么是光程?光程与波程的区别与联系?
光程(Optical Path Length, OPL): 光程是光在介质中传播时的几何路径长度乘以介质的折射率。它反映了光在介质中传播所经历的相位变化。光程可以用公式表示为:
[ L = n \cdot d ]
其中:
- ( L ) 是光程,
- ( n ) 是介质的折射率,
- ( d ) 是光在介质中的几何路径长度。
波程(Wave Path Length): 波程是光波在传播过程中实际走过的物理距离,通常指的是光在真空中传播的距离。
区别与联系:
- 光程考虑了介质的折射率,而波程只考虑光在真空中的传播距离。
- 光程与波程在真空中是相等的,因为真空的折射率 ( n = 1 )。
- 在介质中,光程等于波程乘以介质的折射率。
- 光程是用来描述光在不同介质中传播时的相位变化的一个重要概念,波程则是光在真空中传播的物理距离。
2. 光的干涉的条件是什么?
光的干涉是指两束或多束相干光相遇时,产生的光强分布的变化。光的干涉需要满足以下条件:
- 相干光源: 光源必须是相干的,即光波之间具有恒定的相位差。通常,这意味着光波必须来自同一光源或通过分光产生。
- 相同频率: 干涉光波必须具有相同的频率(或波长)。
- 相同偏振状态: 干涉光波的偏振状态必须相同或固定。
- 相遇: 干涉光波必须在空间中相遇并重叠。
3. 杨氏双缝干涉条纹分布特点?
��杨氏双缝干涉实验通过两条狭缝产生两束相干光,形成干涉条纹。其特点包括:
-
条纹间距: 干涉条纹的间距与光的波长和双缝间距有关。条纹间距 ( \Delta y ) 可以用以下公式表示:
\[ \Delta y = \frac{\lambda D}{d} \]
其中:
- ( \lambda ) 是光的波长,
- ( D ) 是双缝到屏幕的距离,
- ( d ) 是双缝间距。
-
中央亮条纹: 中央亮条纹最亮且位于两缝的连线的正对面。
-
等间距条纹: 条纹是等间距的亮暗条纹,亮条纹和暗条纹交替出现。
-
条纹强度: 中央亮条纹强度最大,向两侧逐渐减弱。
4. 什么是等倾干涉?
等倾干涉(Equal Inclination Interference): 等倾干涉是指光在具有平行表面的薄膜(如肥皂泡、光学薄膜)上反射后形成的干涉现象。由于薄膜的两表面平行,反射光束的入射角相同,导致干涉条纹呈现出等倾角的特点。
5. 等倾干涉条纹的特点?
等倾干涉条纹的特点包括:
- 同心圆环: 条纹通常呈现为同心圆环状,中心是亮��条纹或暗条纹,具体取决于薄膜的厚度和光的波长。
- 条纹间距: 条纹间距与薄膜的厚度和光的波长有关。薄膜厚度越大,条纹间距越小。
- 颜色变化: 当白光照射时,由于不同波长光的干涉条件不同,条纹会呈现出彩虹般的颜色变化。
- 对称性: 条纹关于薄膜的中心对称,且条纹的形状和分布与薄膜的几何形状有关。
这些特点是由光在薄膜表面反射和干涉的物理过程决定的。
第十周简答题
好的,让我们从大学物理的角度详细回答这些问题。
1. 什么叫增透膜、增反膜?
增透膜(Anti-reflective coating): 增透膜是一种薄的光学涂层,通常由一种或多种纳米级厚度的透明材料构成,涂覆在透镜或其他光学元件的表面。其主要作用是通过干涉效应减少光在界面的反射,从而增加透射光的强度。典型的增透膜设计会使得入射光在膜层与基底界面产生的反射光波与在膜层表面产生的反射光波相互抵消(相位相差为半波长),从而减小反射。
增反膜(Reflective coating): 增反膜则是通过在光学元件表面涂覆一层或多层具有高反射率的材料,增加光的反射率,减少透射光的强度。增反膜常用于镜子、激光腔镜等需要高反射率的光学元件中。增反膜的设计通常通过�多层膜的干涉效应来增强反射光波的强度。
2. 相机镜头为什么呈紫红色?
相机镜头呈现紫红色通常是由于镜头表面涂有增透膜。增透膜通过选择性减少某些波长光的反射,增加透射光的强度,从而提高镜头的透光率和成像质量。由于增透膜的干涉效应,某些波长的光(通常是蓝光和绿色光)被更有效地透射,而其他波长的光(如红光和紫光)则会部分反射,从而使得镜头在某些角度下呈现紫红色的反射光。
3. 夫朗禾费衍射与菲涅尔衍射区别?
夫朗禾费衍射(Fraunhofer Diffraction):
- 发生在远场条件下,即光源和观察屏幕距离足够远,或者通过透镜将光聚焦到远处。
- 衍射图样是平行光束的干涉结果,通常在焦平面上观察。
- 数学处理相对简单,可以用傅里叶变换描述。
菲涅尔衍射(Fresnel Diffraction):
- 发生在近场条件下,即光源或观察屏幕距离障碍物较近。
- 衍射图样是球面波的干涉结果,图样随距离变化显著。
- 数学处理较复杂,需要用菲涅尔积分描述。
4. 什么是半波带法?
半波带法(Half-period zones method)是分析光衍射的一种方法,尤其用于描述圆孔或圆形光阑的衍射。将光波前分成多个同心圆环,每个环的光程相差半个波长(即相位相差180度)。这些环称为半波带。由于相邻半波带的光相位相差180度,理论上每两个相邻半波带的光会相互干涉抵消,从而影响衍射图样的强度分布。
5. 半波带个数如何决定?
半波带的个数取决于观察点到光源或光阑的距离以及光波的波长。具体来说,半波带的个数 ( N ) 可以由以下公式近似计算:
其中:
- ( r ) 是从光源到观察点的径向距离,
- ( \lambda ) 是光的波长,
- ( z ) 是光源到光阑的轴向距离。
6. 单缝衍射条纹特点?
单缝衍射条纹的特点包括:
- 中央亮条纹最宽且最亮,强度最大。
- 中央亮条纹两侧是交替出现的暗条纹和较窄的亮条纹,亮条纹的强度逐渐减弱。
- 条纹间距与缝宽、光波波长和观察距离有关,缝宽越窄,条纹间距越大。
- 亮条纹和暗条纹的位置可以通过以下公式确定:
- 亮条纹(最大值): ( d \sin \theta = m \lambda )(其中 ( m ) 为整数)
- 暗条纹(最小值): ( d \sin \theta = (m + \frac12) \lambda )(其中 ( m ) 为整数)
这些特点是由光的波动性和干涉效应共同决定的。
第十一周简答题
好的,让我们从大学物理的角度详细回答这些问题。
1. 光栅衍射与单缝衍射关系?
单缝衍射: 单缝衍射是当光通过一个狭缝时发生的衍射现象。光波在狭缝的边缘发生弯曲,导致在屏幕上形成一系列明暗相间的条纹。中央条纹最亮,强度最大,两侧的条纹强度逐渐减弱。
光栅衍射: 光栅衍射是当光通过一个具有大量平行狭缝的光栅时发生的衍射现象。光栅的每个狭缝都会产生类似单缝衍射的效果,但由于多个狭缝的干涉,光栅衍射的条纹图样更为复杂和清晰。
关系:
- 单缝衍射的条纹图样是光栅衍射条纹图样的基本构成单元。光栅的每个狭缝都产生单缝衍射图样。
- 光栅衍射的条纹位置由光栅方程决定,而条纹的强度分布由单缝衍射的包络决定。
- 光栅衍射的主极大条纹位置与单缝衍射的极大条纹位置相吻合,但光栅衍射的条纹更窄且更亮。
2. 什么是主极大条纹?
主极大条纹(Principal maxima): 在光栅衍射中,主极大条纹是由光栅方程决定的亮条纹位置。这些条纹是由于所有光栅缝的光波在这些方向上相干叠加,产生强烈的干涉极大。主极大条纹的位置由以下光栅方程确定:
[ d \sin \theta = m \lambda ]
其中:
- ( d ) 是光栅常数(即相邻两狭缝之间的距离),
- ( \theta ) 是衍射角,
- ( m ) 是衍射级次(整数),
- ( \lambda ) 是光的波长。
3. 什么是次极大条纹?
次极大条纹(Secondary maxima): 次极大条纹是光栅衍射图样中位于主极大条纹之间的较弱的亮条纹。这些条纹是由于部分相干的光波在这些方向上叠加产生的,但其强度远小于主极大条纹。次极大条纹的位置和强度与光栅的结构和光的波长有关,但一般不如主极大条纹显著。
4. 光栅衍射条纹特点?
光栅衍射条纹的特点包括:
- 条纹位置由光栅方程确定,条纹间距与光栅常数和光波波长有关。
- 主极大条纹非常亮且窄,条纹强度随衍射级次增加而减弱。
- 次极大条纹较弱且宽,位于主极大条纹之间。
- 条纹的间距与光栅的狭缝数和狭缝间距有关,狭缝数越多,条纹越锐利。
5. 什么是缺级现象?
缺级现象(Missing order): 缺级现象是指在某些特定条件下,光栅衍射的某些衍射级次的主极大条纹消失的现象。这通常发生在光栅的狭缝宽度与光波波长的关系满足特定条件时。缺级现象的出现是因为在这些特定方向上,单缝衍射的最小值与光栅衍射的主极大条纹位置重合,导致该衍射级次的条纹被削弱或完全消失。
6. 什么是光的偏振性?
光的偏振性(Polarization of light): 光的偏振性是指光波的电场矢量在传播方向上的振动方向。未偏振光的电场矢量在所有方向上随机振动,而偏振光的电场矢量在特定方向上振动。根据电场矢量的振动方向,偏振光可以分为线偏振光、圆偏振光和椭圆偏振光。
7. 如何区别偏振光?
区别偏振光的方法包括:
- 偏振滤光片(Polarizing filter): 通过观察光通过偏振滤光片后的强度变化,可以判断光的偏振性。线偏振光通过偏振滤光片时,�其强度会随滤光片的旋转角度变化,而未偏振光的强度变化较小。
- 双折射材料(Birefringent material): 通过双折射材料,如方解石晶体,可以将偏振光分成两束偏振方向不同的光,从而观察其偏振性。
- 反射和折射实验: 利用布儒斯特角(Brewster's angle)现象,入射角等于布儒斯特角时,反射光完全偏振。
8. 马吕斯定理的内容?
马吕斯定理(Malus's Law): 马吕斯定理描述了通过偏振器后的线偏振光的强度变化。定理表明,当线偏振光通过一个偏振片时,透射光的强度 ( I ) 与入射光的强度 ( I_0 ) 和入射光的偏振方向与偏振片透过轴之间的夹角 ( \theta ) 之间的关系为:
\[ I = I_0 \cos^2 \theta \]
这意味着透射光的强度与夹角的余弦平方成正比。
