跳到主要内容

数据结构大作业(关键路径)

丁致宇 202331060205 [TOC]

题目要求​

  1. 活动优先图（AOE）的绘制: 根据给定的电影制作过程，绘制出反映各活动和时间需求的AOE图。该图将作为确定项目时间线和关键路径的基础。

  2. 关键路径分析: 通过分析AOE图，找出决定项目最短完成时间的关键路径。关键路径是项目中不可延误的活动序列，其总时长决定了整个项目的最短完成时间。

  3. 算法实现与结果输出: 实现一个算法来计算从项目启动到开始拍摄的最短时间。此外，算法还需输出关键路径上的具体活动。

  4. 效率分析: 分析所实现算法的时间复杂度和空间复杂度。

具体实现​

绘制AOE图​

graph LR;
    A[项目启动] -->|1| B[确定导演]
    B -->|2| C[完善细节]
    C -->|2| F[开始拍摄]
    A -->|3| D[确定演员]
    B -->|1| D
    D -->|2| F
    A -->|5| E[完成场地确认]
    D -->|1| E
    E -->|1| C
    E -->|2| F

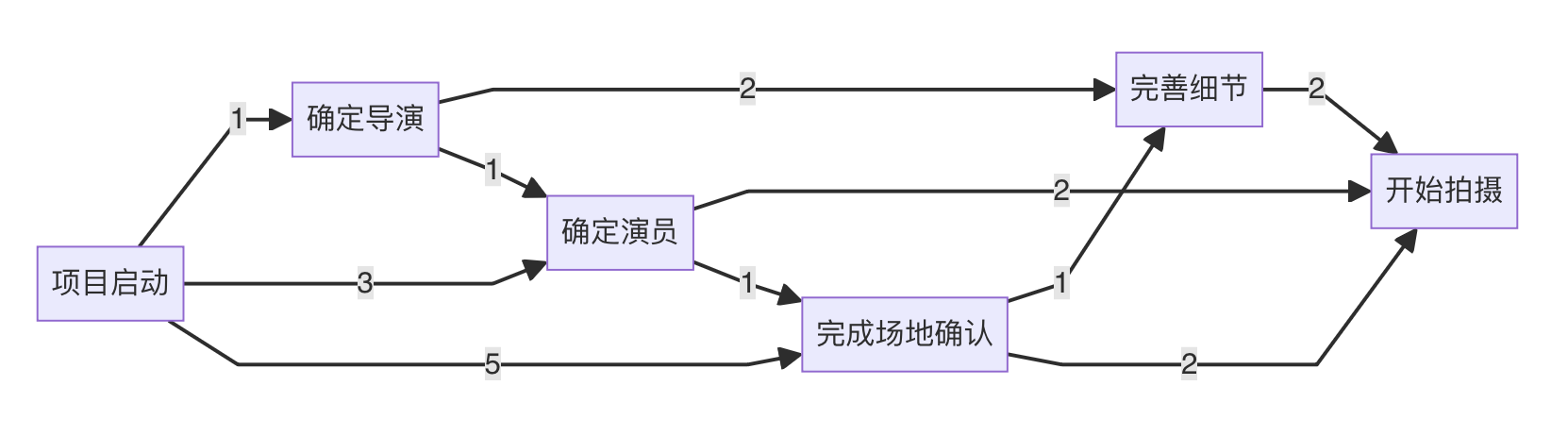
image-20240701211053950

分析关键路径​

  • 0 (项目启动)
  • 1 (确定导演)
  • 2 (完善细节)
  • 3 (确定演员)
  • 4 (完成场地确认)
  • 5 (开始拍摄)

根据边的定义和权重，计算如下路径：

  • 0 -> 1 -> 2 -> 5
  • 0 -> 3 -> 5
  • 0 -> 4 -> 2 -> 5
  • 0 -> 4 -> 5

计算每条路径的总时长，以确定哪条是关键路径。

计算

  • 路径 0 -> 1 -> 2 -> 5: 时间 = 1 + 2 + 2 = 5
  • 路径 0 -> 3 -> 5: 时间 = 3 + 2 = 5
  • 路径 0 -> 4 -> 2 -> 5: 时间 = 5 + 1 + 2 = 8 （最长路径）
  • 路径 0 -> 4 -> 5: 时间 = 5 + 2 = 7

路径 0 -> 4 -> 2 -> 5 是关键路径，因为它具有最长的持续时间，为8个时间单位。任何在这条路径上的延迟都将直接影响整个项目的完成时间。

结论

"项目启动 -> 完成场地确认 -> 完善细节 -> 开始拍摄" 是关键路径

代码实现​

  1. 构建图的数据结构 - 使用邻接表来表示图。
  2. 拓扑排序 - 为了确定活动的先后顺序。
  3. 关键路径法 - 计算最短完成时间。
#include <stdio.h>
#include <stdlib.h>

#define MAX_NODES 6 // 定义最大节点数

int indegree[MAX_NODES] = {0}; // 存储每个节点的入度
int earliest[MAX_NODES] = {0}; // 存储每个节点的最早开始时间
int latest[MAX_NODES] = {0};   // 存储每个节点的最迟开始时间

// 定义节点结构体
typedef struct Node
{
    int vertex;        // 邻接点编号
    int weight;        // 边的权重
    struct Node *next; // 指向下一个邻接点的指针
} Node;

Node *graph[MAX_NODES] = {NULL}; // 图的邻接表表示

// 向图中添加边
void addEdge(int start, int end, int weight)
{
    Node *newNode = (Node *)malloc(sizeof(Node)); // 动态分配节点内存
    newNode->vertex = end;                        // 设置邻接点编号
    newNode->weight = weight;                     // 设置权重
    newNode->next = graph[start];                 // 将新节点插入到链表中
    graph[start] = newNode;
    indegree[end]++; // 增加终点的入度
}

// 将节点编号转换为具体事件名称
const char *translateEvent(int vertex);

// 拓扑排序
void topologicalSort(int *sorted)
{
    int queue[MAX_NODES], front = 0, rear = 0; // 使用队列实现拓扑排序
    for (int i = 0; i < MAX_NODES; i++)
    {
        if (indegree[i] == 0)
        {
            queue[rear++] = i; // 将入度为0的节点入队
        }
    }

    int index = 0;
    while (front < rear)
    {
        int u = queue[front++]; // 出队一个节点
        sorted[index++] = u;    // 存储排序结果
        for (Node *v = graph[u]; v != NULL; v = v->next)
        {
            if (--indegree[v->vertex] == 0)
            {
                queue[rear++] = v->vertex; // 若减少入度后入度为0，则入队
            }
        }
    }
}

// 计算关键路径
void criticalPath(int *sorted)
{
    for (int i = 0; i < MAX_NODES; i++)
    {
        int u = sorted[i];
        for (Node *v = graph[u]; v != NULL; v = v->next)
        {
            if (earliest[v->vertex] < earliest[u] + v->weight)
            {
                earliest[v->vertex] = earliest[u] + v->weight; // 计算最早时间
            }
        }
    }

    for (int i = 0; i < MAX_NODES; i++)
    {
        latest[i] = earliest[MAX_NODES - 1]; // 初始化最迟时间
    }

    for (int i = MAX_NODES - 1; i >= 0; i--)
    {
        int u = sorted[i];
        for (Node *v = graph[u]; v != NULL; v = v->next)
        {
            if (latest[u] > latest[v->vertex] - v->weight)
            {
                latest[u] = latest[v->vertex] - v->weight; // 计算最迟时间
            }
        }
    }

    printf("Minimum time to start shooting is %d time units.\n", earliest[MAX_NODES - 1]);
    printf("Critical path includes:\n\n ");
    for (int i = 0; i < MAX_NODES; i++)
    {
        int u = sorted[i];
        for (Node *v = graph[u]; v != NULL; v = v->next)
        {
            if (earliest[u] + v->weight == latest[v->vertex] && earliest[u] == latest[u])
            {
                printf("%s --> %s\n", translateEvent(u), translateEvent(v->vertex)); // 使用事件名称输出关键路径
            }
        }
    }
}

// 将节点编号转换为具体事件名称
const char *translateEvent(int vertex)
{
    switch (vertex)
    {
    case 0:
        return "Project Start";
    case 1:
        return "Confirm Director";
    case 2:
        return "Finalize Details";
    case 3:
        return "Confirm Actors";
    case 4:
        return "Complete Locations";
    case 5:
        return "Start Shooting";
    default:
        return "Unknown";
    }
}

int main()
{
    addEdge(0, 1, 1);
    addEdge(1, 2, 2);
    addEdge(2, 5, 2);
    addEdge(0, 3, 3);
    addEdge(1, 3, 1);
    addEdge(3, 5, 2);
    addEdge(0, 4, 5);
    addEdge(3, 4, 1);
    addEdge(4, 2, 1);
    addEdge(4, 5, 2);

    int sorted[MAX_NODES];
    topologicalSort(sorted);
    criticalPath(sorted);
    return 0;
}


代码截图​

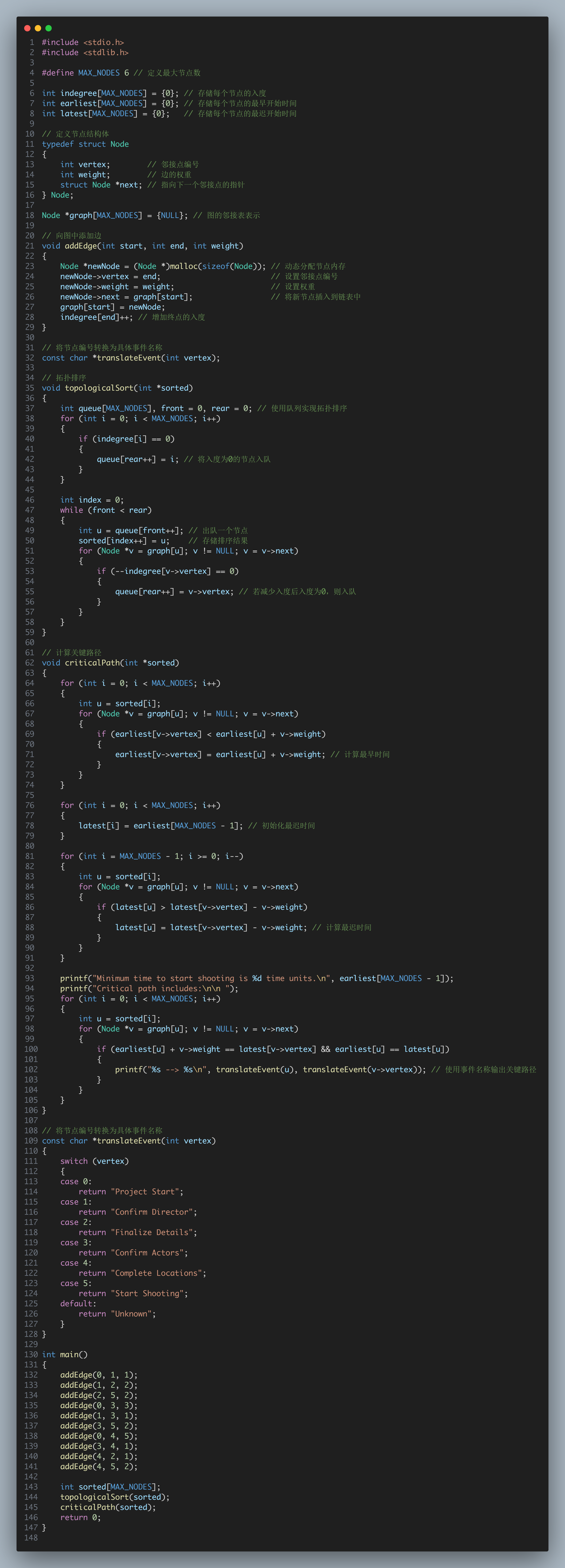
DataStructerWork

运行结果截图​

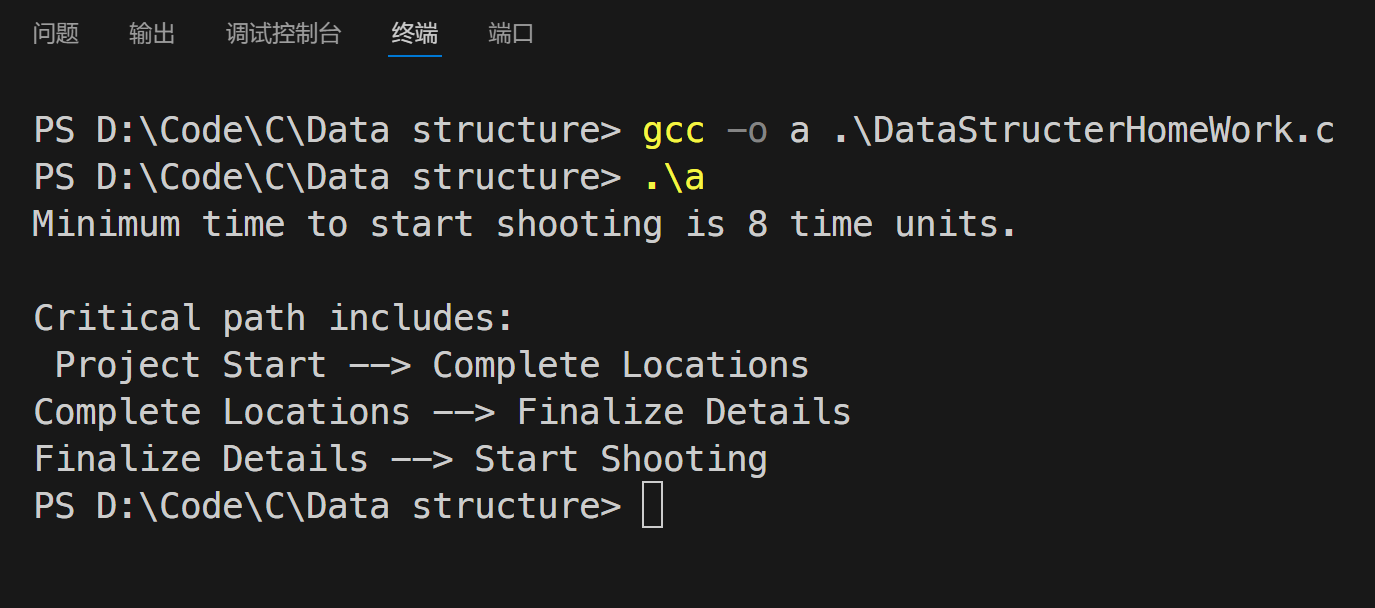
image-20240621010300662

效率分析​

时间复杂度​

  1. 添加边操作 (addEdge): 每次调用addEdge函数的时间复杂度为(O(1))因为它只包括几个基本操作，如分配内存和更新邻接表。

  2. 拓扑排序 (topologicalSort): 在拓扑排序中，每个节点都被放入队列中一次，从队列中出来一次，每个边也被检查一次。如果有( V )个节点和( E )个边，那么拓扑排序的时间复杂度是( O(V + E) )。

  3. 关键路径计算 (criticalPath): 这部分涉及两次遍历所有的边和节点：一次是计算最早开始时间，一次是计算最迟开始时间。因此，这部分的时间复杂度也是( O(V + E) )。

综合来看，整个算法的时间复杂度为( O(V + E) )。

空间复杂度​

  1. 邻接表: 使用邻接表存储图结构，对于每个节点，都有一个链表来存储连接的边。所以空间复杂度与节点和边的数量有关，为( O(V + E) )。

  2. 辅助数组: 如indegree, earliest, latest, 和sorted，每个都占用( O(V) )的空间。

  3. 队列: 在拓扑排序中使用的队列，最坏情况下可以包含图中的所有节点，因此需要( O(V) )的空间。

因此，整个算法的空间复杂度主要由邻接表和辅助数据结构组成，总的来说是( O(V + E) )。