数据结构08-汉诺塔问题

代码

#include <stdio.h>

/**
 * 汉诺塔问题函数。
 * @param paraN 盘子的数量
 * @param paraSource 起始柱子
 * @param paraDestination 目标柱子
 * @param paraTransit 中转柱子
 */
void hanoi(int paraN, char paraSource, char paraDestination, char paraTransit) {
    // 如果没有盘子，则不进行操作
	if (paraN <= 0) {
		return;
	} else {
        // 移动上面的n-1个盘子到中转柱子
		hanoi(paraN - 1, paraSource, paraTransit, paraDestination);
        // 移动剩下的盘子到目标柱子
		printf("%c -> %c \r\n", paraSource, paraDestination);
        // 再将中转柱子上的n-1个盘子移动到目标柱子
		hanoi(paraN - 1, paraTransit, paraDestination, paraSource);
	}// Of if
}// Of hanoi

/**
 * 测试汉诺塔函数。
 */
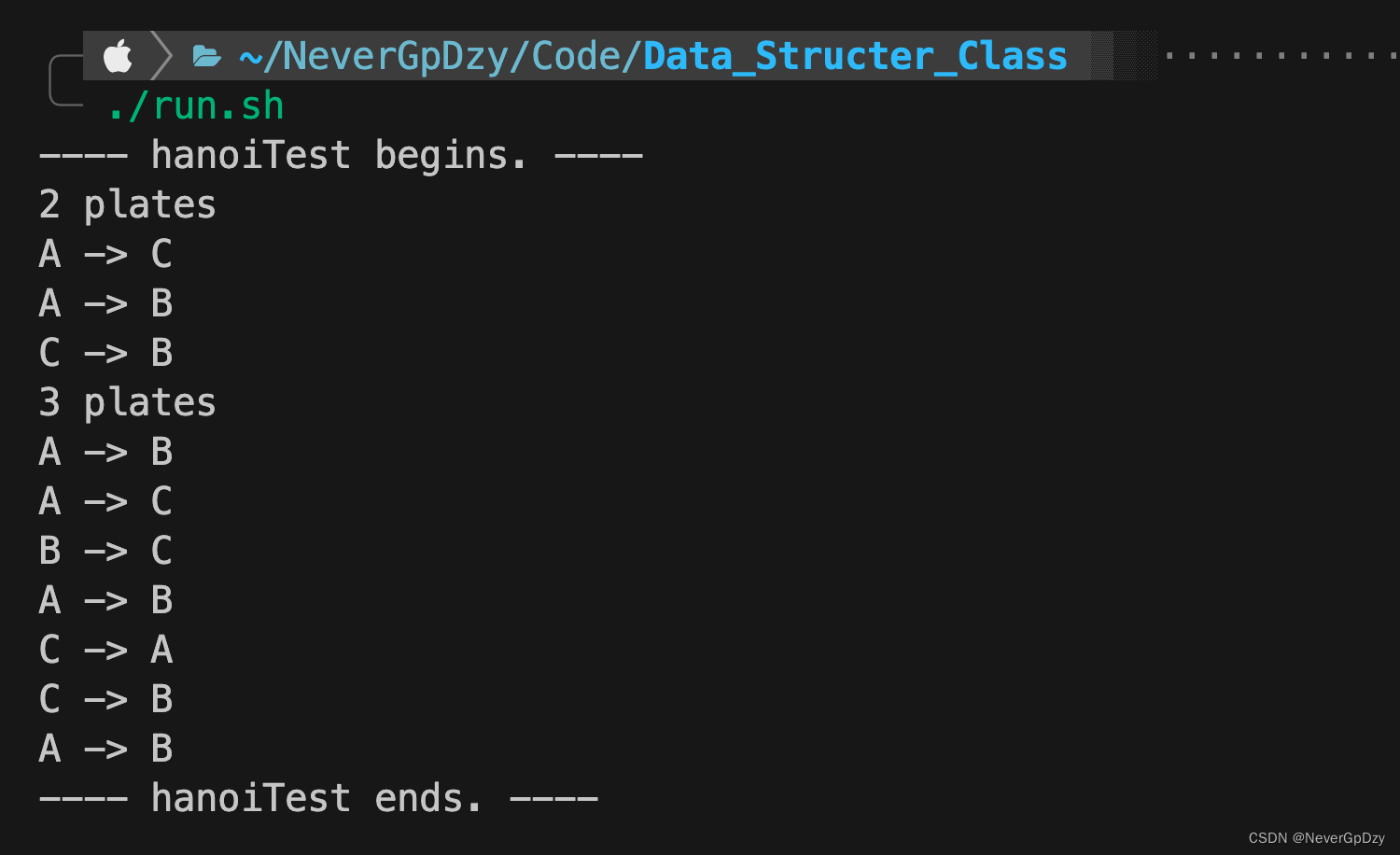
void hanoiTest() {
    printf("---- hanoiTest begins. ----\r\n");

    // 测试2个盘子的情况
	printf("2 plates\r\n");
	hanoi(2, 'A', 'B', 'C');

    // 测试3个盘子的情况
	printf("3 plates\r\n");
	hanoi(3, 'A', 'B', 'C');

    printf("---- hanoiTest ends. ----\r\n");
}// Of hanoiTest

/**
 * 主函数。
 */
void main() {
    // 运行汉诺塔测试
	hanoiTest();
}// Of main

总结： 这段代码是一个简单的汉诺塔问题的解决方案。汉诺塔问题是一个经典的递归问题，目标是将一堆大小不一的盘子从一个柱子移动到另一个柱子，期间只能小盘子在上，大盘子在下，并且每次只能移动一个盘子。

• hanoi 函数通过递归的方式来解决问题，它将问题分解为更小的子问题，直到没有盘子需要移动。
• hanoiTest 函数用来测试 hanoi 函数，它测试了2个盘子和3个盘子的情况。
• main 函数是程序的入口点，它调用 hanoiTest 函数来执行测试。

分析

时间复杂度O(2^n) 空间复杂度O(n)

运行结果