3.3 并行性表现

【CUDA 基础】3.3 并行性表现

发表于 2018-04-15 | 分类于 CUDA，Freshman | 评论数： 0 | 阅读次数：

Abstract: 本文主要通过nvprof工具来分析核函数的执行效率（资源利用率）

Keywords: nvprof

并行性表现

继续更新CUDA，前面为了加速概率论的学习暂停了一段时间的CUDA，从今天开始继续CUDA和数学分析的更新，每一篇都写一点废话就相当于自己的日记了。之前很佩服那些写日记的人，因为根本不知道日记可以写些什么，但是现在看看，如果写一些文字来记录自己，首先可以反思当下，其次是过一段时间以后可以看看自己到底有没有进步，这些都是有用的，所以大家可以略过我的废话，直接看正文。

本文的主要内容就是进一步理解线程束在硬件上执行的本质过程，结合上几篇关于执行模型的学习，本文内容相对简单，通过修改核函数的配置，来观察核函数的执行速度，以及分析硬件利用数据，分析性能。调整核函数配置是CUDA开发人员必须掌握的技能，本篇只研究核函数的配置是如何影响效率的（也就是通过网格、块的配置来获得不同的执行效率）。

本文全文只用到下面的核函数：

__global__ void sumMatrix(float * MatA, float * MatB, float * MatC, int nx, int ny)
{
    int ix = threadIdx.x + blockDim.x * blockIdx.x;
    int iy = threadIdx.y + blockDim.y * blockIdx.y;
    int idx = ix + iy * ny;
    if (ix < nx && iy < ny)
    {
        MatC[idx] = MatA[idx] + MatB[idx];
    }
}

没有任何优化的最简单的二维矩阵加法。

全部代码：

int main(int argc, char** argv)
{
    //printf("strating...\n");
    //initDevice(0);
    int nx = 1 << 13;
    int ny = 1 << 13;
    int nxy = nx * ny;
    int nBytes = nxy * sizeof(float);

    //Malloc
    float* A_host = (float*)malloc(nBytes);
    float* B_host = (float*)malloc(nBytes);
    float* C_host = (float*)malloc(nBytes);
    float* C_from_gpu = (float*)malloc(nBytes);
    initialData(A_host, nxy);
    initialData(B_host, nxy);

    //cudaMalloc
    float *A_dev = NULL;
    float *B_dev = NULL;
    float *C_dev = NULL;
    CHECK(cudaMalloc((void**)&A_dev, nBytes));
    CHECK(cudaMalloc((void**)&B_dev, nBytes));
    CHECK(cudaMalloc((void**)&C_dev, nBytes));

    CHECK(cudaMemcpy(A_dev, A_host, nBytes, cudaMemcpyHostToDevice));
    CHECK(cudaMemcpy(B_dev, B_host, nBytes, cudaMemcpyHostToDevice));

    int dimx = argc > 2 ? atoi(argv[1]) : 32;
    int dimy = argc > 2 ? atoi(argv[2]) : 32;

    double iStart, iElaps;

    // 2d block and 2d grid
    dim3 block(dimx, dimy);
    dim3 grid((nx-1)/block.x+1, (ny-1)/block.y+1);
    iStart = cpuSecond();
    sumMatrix<<<grid, block>>>(A_dev, B_dev, C_dev, nx, ny);
    CHECK(cudaDeviceSynchronize());
    iElaps = cpuSecond() - iStart;
    printf("GPU Execution configuration<<<(%d,%d),(%d,%d)|%f sec\n",
           grid.x, grid.y, block.x, block.y, iElaps);
    CHECK(cudaMemcpy(C_from_gpu, C_dev, nBytes, cudaMemcpyDeviceToHost));

    cudaFree(A_dev);
    cudaFree(B_dev);
    cudaFree(C_dev);
    free(A_host);
    free(B_host);
    free(C_host);
    free(C_from_gpu);
    cudaDeviceReset();
    return 0;
}

可见我们用两个 8192×8192 的矩阵相加来测试我们的效率。

注意一下这里的GPU内存，一个矩阵是 2^13×2^13×2^2=2^28 字节，也就是 256M，三个矩阵就是 768M。因为我们的GPU内存就是 2G 的，所以我们没办法进行更大的矩阵计算了（无法使用原文使用的 2^14 的方矩阵）。

用 nvprof 检测活跃的线程束

对比性能要控制变量，上面的代码只用两个变量，也就是块的x和y的大小，所以，调整x和y的大小来产生不同的效率，我们先来看看结果：

图片看不清，数据结果如下：

gridDim	blockDim	time(s)
256,256	32,32	0.008304
256,512	32,16	0.008332
512,256	16,32	0.008341
512,512	16,16	0.008347
512,1024	16,8	0.008351
1024,512	8,16	0.008401

当块大小超过硬件的极限，并没有报错，而是返回了错误值，这个值得大家注意。

另外，每个机器执行此代码效果可能肯定不一样，所以大家要根据自己的硬件分析数据。

书上给出的 M2070 就和我们的结果不同，M2070的 (32,16) 效率最高，而我们的 (32,32) 效率最高，毕竟架构不同，而且CUDA版本不同导致了优化后的机器码差异很大，所以我们还是来看看活跃线程束的情况，使用：

nvprof --metrics achieved_occupancy ./simple_sum_matrix

得出结果：

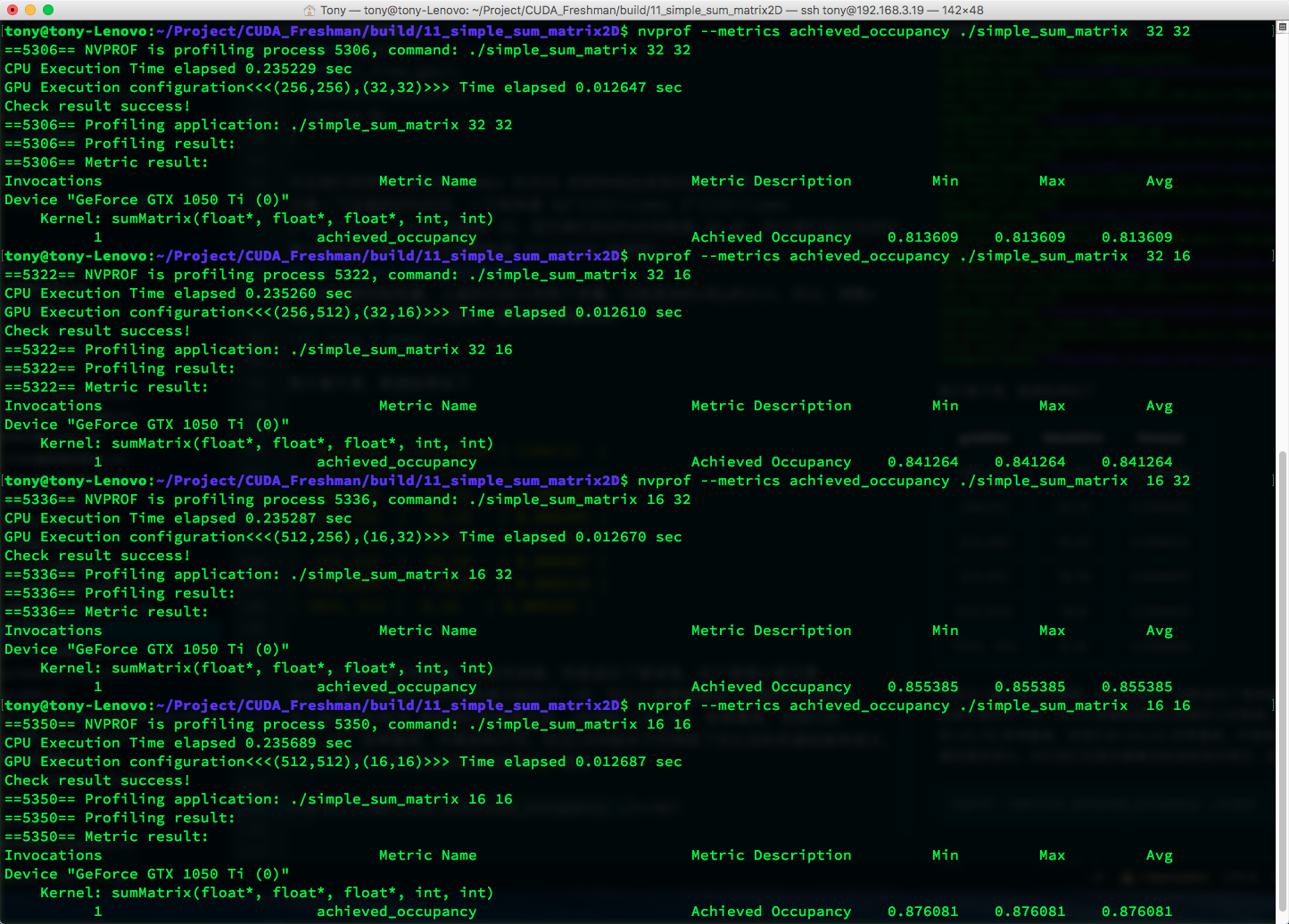
gridDim	blockDim	time(s)	Achieved Occupancy
256,256	32,32	0.008304	0.813609
256,512	32,16	0.008332	0.841264
512,256	16,32	0.008341	0.855385
512,512	16,16	0.008347	0.876081
512,1024	16,8	0.008351	0.875807
1024,512	8,16	0.008401	0.857242

可见活跃线程束比例高的未必执行速度快，但实际上从原理出发，应该是利用率越高效率越高，但是还受到其他因素制约。

活跃线程束比例的定义是：每个周期活跃的线程束的平均值与一个SM支持的线程束最大值的比值。

用 nvprof 检测内存操作

下面我们继续用nvprof来看看内存利用率如何。

首先使用：

nvprof --metrics gld_throughput ./simple_sum_matrix

来看一下内核的内存读取效率：

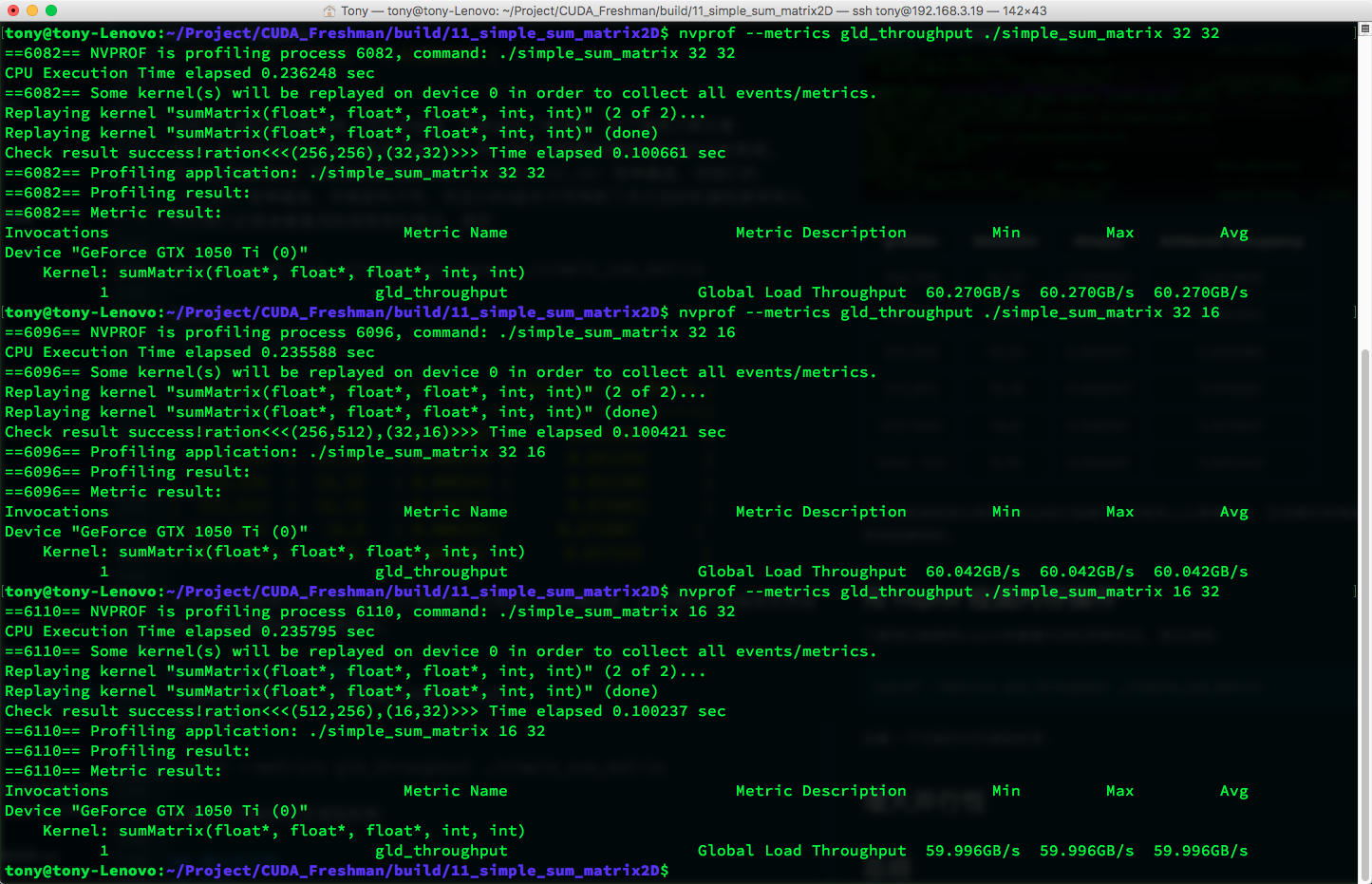
gridDim	blockDim	time(s)	Achieved Occupancy	GLD Throughput (GB/s)
256,256	32,32	0.008304	0.813609	60.270
256,512	32,16	0.008332	0.841264	60.042
512,256	16,32	0.008341	0.855385	59.996
512,512	16,16	0.008347	0.876081	59.967
512,1024	16,8	0.008351	0.875807	59.976
1024,512	8,16	0.008401	0.857242	59.440

可以看出虽然第一种配置的线程束活跃比例不高，但是吞吐量最大，所以可见吞吐量和线程束活跃比例一起都对最终的效率有影响。

接着我们看看全局加载效率，全局加载效率的定义是：被请求的全局加载吞吐量占所需的全局加载吞吐量的比值（全局加载吞吐量），也就是说应用程序的加载操作利用了设备内存带宽的程度。注意区别吞吐量和全局加载效率的区别，这个在前面我们已经解释过吞吐量了，忘了的同学回去看看。

nvprof --metrics gld_efficiency ./simple_sum_matrix

获得如下运行结果：

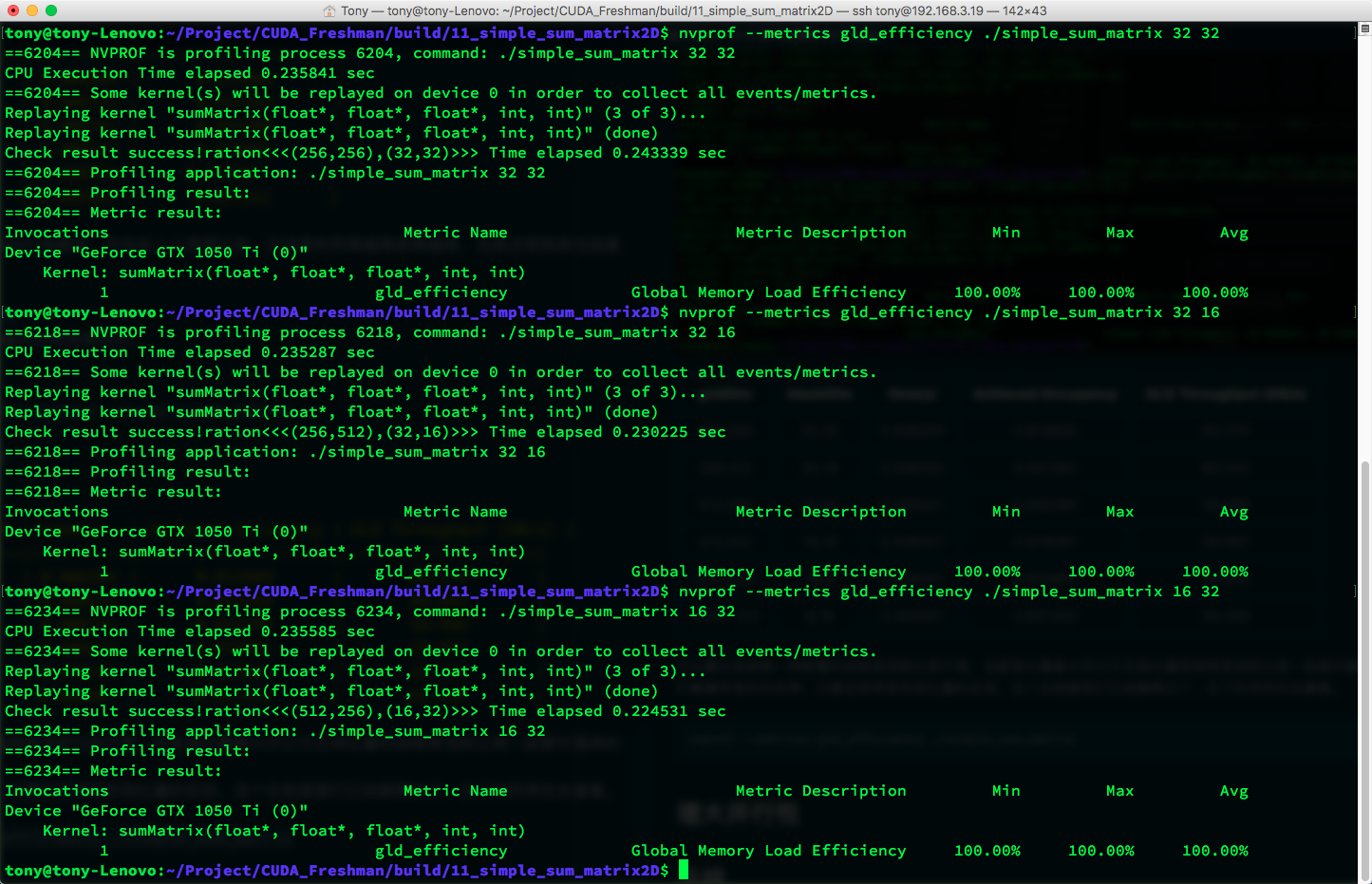
可以看到，在当前机器上进行测试所有的利用率都是 100%，可见CUDA对核函数进行了优化。在 M2070上使用以前的CUDA版本，并没有如此高的加载效率，有效加载效率是指在全部的内存请求中（当前在总线上传递的数据）有多少是我们要用于计算的。

书上说如果线程块中内层的维度（blockDim.x）过小，小于线程束会影响加载效率，但是目前来看，不存在这个问题了。

随着硬件的升级，以前的一些问题，可能就不是问题了，当然对付老的设备，这些技巧还是很有用的。

增大并行性

上面说"线程块中内层的维度（blockDim.x）过小"是否对现在的设备还有影响，我们来看一下下面的试验：

用表格列举一下数据：

gridDim	blockDim	time(s)
(128,4096)	(64,2)	0.008391
(128,2048)	(64,4)	0.008411
(128,1024)	(64,8)	0.008405
(64,4096)	(128,2)	0.008454
(64,2048)	(128,4)	0.008430
(64,1024)	(128,8)	0.008418
(32,4096)	(256,2)	0.008468
(32,2048)	(256,4)	0.008439
(32,1024)	(256,8)	fail

通过这个表我们发现，最快的还是第一个，块最小的反而获得最高的效率，这里与书上的结果又不同了，我想书上的数据量大可能会影响结果，当数据量大的时候有可能决定时间的因素会发生变化，但是一些结果是可以观察到的：

尽管（64，4）和（128，2）有同样大小的块，但是执行效率不同，说明内层线程块尺寸影响效率。
最后的块参数无效
第一种方案速度最快

我们调整块的尺寸，还是为了增加并行性，或者说增加活跃的线程束，我们来看看线程束的活跃比例：

得到如下数据：

gridDim	blockDim	time(s)	Achieved Occupancy
(128,4096)	(64,2)	0.008391	0.888596
(128,2048)	(64,4)	0.008411	0.866298
(128,1024)	(64,8)	0.008405	0.831536
(64,4096)	(128,2)	0.008454	0.893161
(64,2048)	(128,4)	0.008430	0.862629
(64,1024)	(128,8)	0.008418	0.833540
(32,4096)	(256,2)	0.008468	0.859110
(32,2048)	(256,4)	0.008439	0.825036
(32,1024)	(256,8)	fail	Nan

可见最高的利用率没有带来最高的效率。

没有任何一个因素可以直接左右最后的效率，一定是多个因素一起作用得到最终的结果，这是多因一效的典型例子。因此在优化的时候，我们应该首先保证测试时间的准确性、客观性，以及稳定性，说实话，我们上面的时间测试方法并不那么稳定，更稳定的方法应该是测几次的平均时间，来降低人为误差。

总结

指标与性能：

大部分情况，单一指标不能优化出最优性能
总体性能直接相关的是内核的代码本质（内核才是关键）
指标与性能之间需要选择平衡点
从不同的角度寻求指标平衡，最大化效率
网格和块的尺寸为调节性能提供了一个不错的起点

从这个起点开始，我们后面逐渐深入到各项指标，总之，用CUDA就是为了高效，而研究这些指标是提高效率最快的途径（当然内核算法提升空间更大）。再强调一下，本文的所有数据只针对我使用的设备，对于任何其他的设备这些数据会完全不同，大家主要学习这几个测试指标和其间的相互关系。

【CUDA 基础】3.3 并行性表现​

并行性表现

用 nvprof 检测活跃的线程束​

用 nvprof 检测内存操作​

增大并行性​

总结​

【CUDA 基础】3.3 并行性表现

用 nvprof 检测活跃的线程束

用 nvprof 检测内存操作

增大并行性

总结